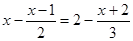一个不透明的袋子中装有4个质地、大小均相同的小球,这些小球上分别标有数字3、4、5、x.甲、乙两人每次从袋中各随机摸出1球,并计算摸出这2个小球上数字之和,记录后都将放回袋中搅匀,进行重复实验.实验数据如下表:
| 摸球总次数 |
10 |
20 |
30 |
60 |
90 |
120 |
180 |
240 |
330 |
450 |
| “和为8”出现频数 |
2 |
10 |
13 |
24 |
30 |
37 |
58 |
82 |
110 |
150 |
| “和为8”出现频率 |
0.20 |
0.50 |
0.43 |
0.40 |
0.33 |
0.31 |
0.32 |
0.34 |
0.33 |
0.33 |
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为8”频率将稳定在它概率附近.估计
出现“和为8”概率是________.
0.33
(2)如果摸出的这两个小球上数字之和为9概率是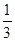 ,那么x值可以取7吗?请用列表法或画树状图法说明理由;如果x值不可以取7,请写出一个符合要求x值.
,那么x值可以取7吗?请用列表法或画树状图法说明理由;如果x值不可以取7,请写出一个符合要求x值.
某学校准备组织部分教师到杭州旅游,现联系了甲、乙两家旅行社,两家旅行社的报价均为400元/人,同时两家旅行社都对10人以上的团体推出了优惠:甲旅行社对每位教师七五折优惠;而乙旅行社是免去一位带队教师的费用,其余教师八折优惠.
(1)若设参加旅游的教师共有x(x>10)人,则甲旅行社的费用为_______元,乙旅行社的费用为_______元;(用含x的代数式表示,并化简)
(2)假如某校组织17名教师到杭州旅游,该校选择哪一家旅行社比较优惠?请说明理由;
(3)若计划在10月份之内外出旅游五天,设最中间一天的日期为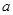 ,求这五天的日期之和(用含
,求这五天的日期之和(用含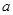 的代数式表示,并化简),假如这五天的日期之和为30的倍数.则他们可能于10月几号出发(请写出简单的求解过程)?
的代数式表示,并化简),假如这五天的日期之和为30的倍数.则他们可能于10月几号出发(请写出简单的求解过程)?
结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是;表示-3和2两点之间的距离是;一般地,数轴上表示数m和数n的两点之间的距离等于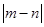 .如果表示数
.如果表示数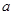 和-2的两点之间的距离是3,那么
和-2的两点之间的距离是3,那么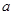 =;
=;
(2)若数轴上表示数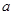 的点位于-4与2之间,求
的点位于-4与2之间,求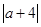 +
+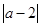 的值;
的值;
有长为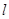 的篱笆,利用它和房屋的一面墙围成如图形状的园子,园子的宽为
的篱笆,利用它和房屋的一面墙围成如图形状的园子,园子的宽为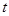 .
.
(1)利用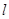 ,
,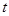 的代数式表示园子的面积;
的代数式表示园子的面积;
(2)当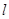 =80米,
=80米,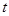 =15米时,求园子的面积。
=15米时,求园子的面积。
把数轴画完整,并在在数轴上表示下列各数,然后按从小到大的顺序用“<”号连接.
-3, 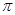 , 2,
, 2, 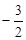 .
.
解方程:① 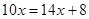 ②
②