如图,在平面直角坐标系中,顶点为(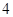 ,
,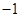 )的抛物线交
)的抛物线交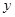 轴于
轴于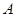 点,交
点,交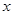 轴于
轴于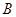 ,
,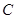 两点(点
两点(点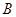 在点
在点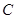 的左侧), 已知
的左侧), 已知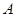 点坐标为(
点坐标为( ,
,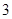 )。
)。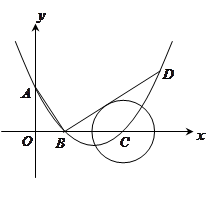
(1)求此抛物线的解析式;
(2)过点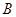 作线段
作线段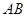 的垂线交抛物线于点
的垂线交抛物线于点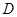 , 如果以点
, 如果以点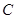 为圆心的圆与直线
为圆心的圆与直线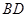 相切,请判断抛物线的对称轴
相切,请判断抛物线的对称轴 与⊙
与⊙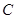 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;
(3)已知点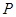 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于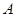 ,
,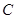 两点之间,过点
两点之间,过点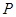 作
作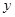 轴的平行线与
轴的平行线与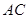 交于点
交于点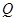 问:当点
问:当点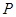 运动到什么位置时,线段
运动到什么位置时,线段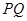 的长度最大?并求出此时△
的长度最大?并求出此时△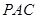 的面积。
的面积。
先化简,再求值: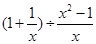 ,其中x=2.
,其中x=2.
尺规作图:画出线段AB的垂直平分线(不写作法,保留作图痕迹)
解方程组 .
.
在平面直角坐标系中,点O为原点,抛物线y=ax2+bx(其中-1≤a<0)经过A(3,n),AB⊥y轴于B,抛物线交直线AB于M.
(1)若n=1,AB=3BM,求抛物线所对应的函数关系式;
(2)若n=a+b,抛物线与x轴另一个异于原点的交点为C,过点A作AP∥OM交直线MC于点P,当△OPM的面积最大时,求sin∠MOP的值.
如图,四边形ABCD是⊙O的内接四边形, ,点E、F分别是弦AD、DC上的点.
,点E、F分别是弦AD、DC上的点.
(1)若∠ABE=∠CBF,BE=BF.求证:BD是⊙O的直径.
(2)若 ,∠D=2∠EBF=90°,AE=ED=2.求DF的长.
,∠D=2∠EBF=90°,AE=ED=2.求DF的长.