设有关于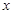 的一元二次方程
的一元二次方程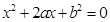 .
.
(1)若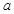 是从
是从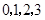 四个数中任取的一个数,
四个数中任取的一个数,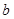 是从
是从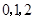 三个数中任取的一个数,求方程有实根的概率.
三个数中任取的一个数,求方程有实根的概率.
(2)若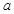 是从区间
是从区间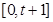 任取的一个数,
任取的一个数,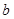 是从区间
是从区间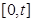 任取的一个数,其中
任取的一个数,其中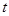 满足
满足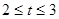 ,求方程有实根的概率,并求出其概率的最大值.
,求方程有实根的概率,并求出其概率的最大值.
某重点高校数学教育专业的三位毕业生甲、乙、丙参加了一所中学的招聘面试,面试合格者可以正式签约,毕业生甲表示只要面试合格就签约,毕业生乙和丙则约定:两人面试都合格就一同签约,否则两人都不签约,设每人面试合格的概率都是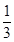 ,且面试是否合格互不影响,求:
,且面试是否合格互不影响,求:
(1)至少有1人面试合格的概率;(2)签约人数X的分布列.
(本题满分10 分)已知函数f(x)=x3-ax2+3x.
(1) 若x=3是f(x)的极值点,求f(x)在x∈[1,a]上的最大值和最小值.
(2) 若f(x)在x∈[1,+∞)上是增函数,求实数a的取值范围;
设复数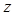 满足
满足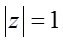 ,且
,且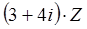 是纯虚数,求
是纯虚数,求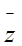 .
.
已知函数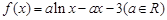 .
.
(I)当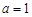 时,求函数
时,求函数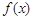 的单调区间;
的单调区间;
(II)若函数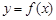 的图象在点
的图象在点 处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的
处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的 ,函数
,函数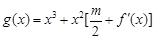 在区间
在区间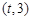 上总存在极值?
上总存在极值?
设椭圆C: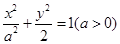 的左、右焦点分别为F1、F2,A是椭圆C上的一点,
的左、右焦点分别为F1、F2,A是椭圆C上的一点,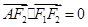 ,坐标原点O到直线AF1的距离为
,坐标原点O到直线AF1的距离为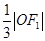 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设Q是椭圆C上的一点,过点Q的直线l 交 x轴于点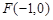 ,交 y轴于点M,若
,交 y轴于点M,若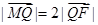 ,求直线l 的斜率.
,求直线l 的斜率.