开学初，小芳和小亮去学校商店购买学习用品，小芳用18元钱买了1支钢笔和3本笔记本；小亮用31元买了同样的钢笔2支和笔记本5本。
（1）求每支钢笔和每本笔记本的价格；
（2）校运会后，班主任拿出200元学校奖励基金交给班长，购买上述价格的钢笔和笔记本共48件作为奖品，奖给校运会中表现突出的同学，要求笔记本数不少于钢笔数，共有多少种购买方案？请你一一写出。
某商场开展购物抽奖活动，抽奖箱中有4个标号分别为1，2，3，4的质地、大小相同的小球，顾客任意摸取一个小球，然后放回，再摸取一个小球，若两次摸出的数字之和为“8”是一等奖，数字之和为“6”是二等奖，数字之和为其他数字则是三等奖，请用列举法分别求出顾客抽中一、二、三等奖的概率．
二次函数
的图象经过点（﹣1，4），且与直线
相交于A、B两点（如图），A点在y轴上，过点B作BC⊥x轴，垂足为点C（﹣3，0）．
（1）求二次函数的表达式；
（2）点N是二次函数图象上一点（点N在AB上方），过N作NP⊥x轴，垂足为点P，交AB于点M，求MN的最大值；
如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD，垂足为E，DA平分∠BDE．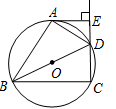
（1）求证：AE是⊙O的切线；
（2）若∠DBC=30°，DE=1㎝，求BD的长．
某工厂生产的某种产品按质量分为10个档次，第1档次（最低档次）的产品一天能生产95件，每件利润6元．每提高一个档次，每件利润增加2元，但一天产量减少5件．
（1）若生产第x档次的产品一天的总利润为y元（其中x为正整数，且1≤x≤10），求出y关于x的函数关系式；
（2）若生产第x档次的产品一天的总利润为1120元，求该产品的质量档次．
如果二次函数的二次项系数为l，则此二次函数可表示为
，我们称[p，q]为此函数的特征数，如函数
的特征数是[2，3]．
（1）若一个函数的特征数为[﹣2，1]，求此函数图象的顶点坐标．
（2）若一个函数的特征数为[4，﹣1]，将此函数的图象先向右平移1个单位，再向上平移1个单位，求得到的图象对应的函数的特征数．