某厂家新开发一种摩托车如图所示,它的大灯A射出的光线AB、AC与地面MN的夹角分别为8°和10°,大灯A与地面距离1 m.该车大灯照亮地面的宽度BC约是多少?
一般正常人从发现危险到做出刹车动作的反应时间是0.2 s,从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离,某人以60km/h的速度驾驶该车,突然遇到危险情况,立即刹车直到摩托车停止,在这过程中刹车距离是
 m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.(参考数据:
m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.(参考数据: ,
, ,
, ,
, )
)
如图,在△ABC中,AE是BC边上的高,AD是角平分线。若∠B=42°,∠C=68°.求∠DAE的度数;
若∠B=
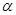 ,∠C=
,∠C= ,用含
,用含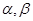 的代数式表示∠DAE.
的代数式表示∠DAE.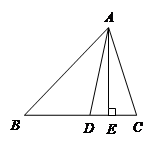
如图,若在△ABC和△DEF中,已知边AB=5,AC=6,DE=6,DF=8,三角形的内角∠A=50°∠B=70°,∠D=40°,∠E=120°,若设△ABC的面积为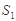 ,△DEF的面积为
,△DEF的面积为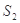 ,则
,则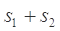 等于▲。
等于▲。
数学课上,李老师出示了如下框中的题目.小敏与同桌小聪讨论后,进行了如下解答:
特殊情况,探索结论
当点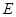 为
为 的中点时,如图1,确定线段
的中点时,如图1,确定线段 与
与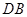 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论:
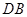 (填“>”,“<”或“=”).
(填“>”,“<”或“=”).特例启发,解答题目
解:题目中, 与
与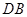 的大小关系是:
的大小关系是:
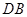 (填“>”,“<”或“=”).理由如下:如图2,过点
(填“>”,“<”或“=”).理由如下:如图2,过点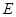 作
作 ,交
,交 于点
于点 .
.
(请你完成以下解答过程)拓展结论,设计新题
在等边三角形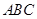 中,点
中,点 在直线
在直线 上,点
上,点 在直线
在直线 上,且
上,且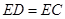 .若
.若 的边长为1,
的边长为1,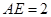 ,求
,求 的长(请你直接写出结果).
的长(请你直接写出结果).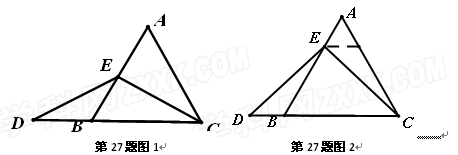
2008年5月1日,目前世界上最长的跨海大桥——杭州湾跨海大桥通车了.通车后,苏南A地到宁波港的路程比原来缩短了l 20千米.已知运输车速度不变时,行驶时间将从原来的3时20分缩短到2时.求A地经杭州湾跨海大桥到宁波港的路程.
A地准备开辟宁波方向的外运路线,即货物从A地经杭州湾跨海大桥到宁波港,再从宁波港运到B地.若有一批货物(不超过10车)从A地按外运路线运到B地的运费需8320元,其中从A地经杭州湾跨海大桥到宁波港的每车运输费为380元,从宁波港到B地的海上运费对一批不超过10车的货物计费方式是:一车800元,当货物每增加l车时,每车的海上运费就减少20元.问这批货物有几车?
已知关于x的一元二次方程
求证:无论
 取任何实数,方程总有实数根;
取任何实数,方程总有实数根;若等腰三角形的一边长为5,另两边长恰好是这个方程的两个根,求这个等腰三角形的周长