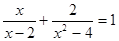两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=2.
固定△ABC不动,将△DEF进行如下操作:如图(1),△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,它的面积是否变化,如果不变请求出 其面积.如果变化,说明理由.
如图(2),当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由
如图(3),△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,
使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出 的值.
的值.


分解因式:
解不等式组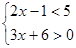 ,并把解集在数轴上表示出来。
,并把解集在数轴上表示出来。
如图,四边形ABCD、CDEF、EFGH都是正方形.
(1) ACF与
ACF与 ACG相似吗?说说你的理由.
ACG相似吗?说说你的理由.
(2)求∠1+∠2的度数.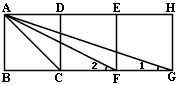
西安某中学初2010级上周刚刚举行了初二下体育期末考试,现随机抽取了部分学生的成绩为样本,按  (优秀)、
(优秀)、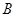 (良好)、
(良好)、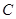 (及格)、
(及格)、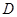 (不及格)四个等级进行统计,并将统计结果制成如下统计图.如图,请你结合图表所给信息解答下列问题:
(不及格)四个等级进行统计,并将统计结果制成如下统计图.如图,请你结合图表所给信息解答下列问题:
(1)本次调查共随机抽取了名学生;
(2)将条形统计图在图中补充完整;
(3)扇形统计图中“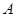 ”部分所对应的圆心角的度数是;
”部分所对应的圆心角的度数是;
(4)若随机抽取一名学生的成绩在等级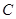 的概率是;
的概率是;
(5)初2012级目前举行了四次体育期末考试,分别是初一上期体育期末考试、初一下期体育期末考试、初二上期体育期末考试、初二下期体育期末考试.学生小欣初一下期体育期末考试成绩为25分,初二下期体育期末考试成绩为36分,若每次体育期末考试小欣体育成绩的增长率相同,求出这个增长率.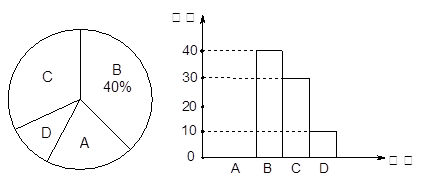
解方程: