阅读以下例题:“解不等式: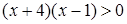
解:①当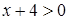 ,则
,则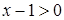 当若
当若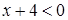 ,则
,则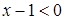
即可以写成: 即可以写成:
即可以写成:
解不等式组得: 解不等式组得:
解不等式组得:
综合以上两种情况:不等式解集: 或
或 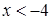
(以上解法依据:若 ,则
,则 同号)请你模仿例题的解法,解不等式:
同号)请你模仿例题的解法,解不等式:
(1) (2)
(2)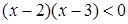
小云在学习过程中遇到一个函数 .
下面是小云对其探究的过程,请补充完整:
(1)当 时,对于函数 ,即 ,当 时, 随 的增大而 ,且 ;对于函数 ,当 时, 随 的增大而 ,且 ;结合上述分析,进一步探究发现,对于函数 ,当 时, 随 的增大而 .
(2)当 时,对于函数 ,当 时, 与 的几组对应值如下表:
|
|
0 |
|
1 |
|
2 |
|
3 |
|
|
|
0 |
|
|
|
1 |
|
|
|
结合上表,进一步探究发现,当 时, 随 的增大而增大.在平面直角坐标系 中,画出当 时的函数 的图象.
(3)过点 , 作平行于 轴的直线 ,结合(1)(2)的分析,解决问题:若直线 与函数 的图象有两个交点,则 的最大值是 .

如图, 为 的直径, 为 延长线上一点, 是 的切线, 为切点, 于点 ,交 于点 .
(1)求证: ;
(2)若 , ,求 的长.

在平面直角坐标系 中,一次函数 的图象由函数 的图象平移得到,且经过点 .
(1)求这个一次函数的解析式;
(2)当 时,对于 的每一个值,函数 的值大于一次函数 的值,直接写出 的取值范围.
如图,菱形 的对角线 , 相交于点 , 是 的中点,点 , 在 上, , .
(1)求证:四边形 是矩形;
(2)若 , ,求 和 的长.

已知:如图, 为锐角三角形, , .
求作:线段 ,使得点 在直线 上,且 .
作法:①以点 为圆心, 长为半径画圆,交直线 于 , 两点;
②连接 .
线段 就是所求作的线段.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明: ,
.
,
点 在 上.
又 点 , 都在 上,
(填推理的依据).
.
