有四张形状、大小和质地相同的卡片A、B、C、D，正面分别写有-优题课

有四张形状、大小和质地相同的卡片A、B、C、D，正面分别写有一个正多边形(所有正多边形的边长相等)，把四张卡片洗匀后正面朝下放在桌面上，从中随机抽取一张(不放回)，接着再随机抽取一张．

请你用画树形图或列表的方法列举出可能出现的所有结果；
如果在(1)中各种结果被选中的可能性相同，求两次抽取的正多边形能构成平面镶嵌的概率；
若两种正多边形构成平面镶嵌，p、q表示这两种正多边形的个数，x、y表示对应正多边形的每个内角的度数，则有方程px＋qy＝360，求每种平面镶嵌中p、q的值．

科目数学题型解答题难度中等

知识点：利用频率估计概率

（1）计算： $\frac{x + 1}{x^{2} - 1} \div \frac{2}{x - 1}$ ；

（2）如图，正方形 $ABCD$ 中，点 $E$ ， $F$ ， $G$ 分别在 $AB$ ， $BC$ ， $CD$ 上，且 $∠ EFG = 90 °$ ．求证： $ΔEBF ∽ ΔFCG$ ．

如图，抛物线 $y = a x^{2} + \frac{1}{2} x + c$ 交 $x$ 轴于 $A$ ， $B$ 两点，交 $y$ 轴于点 $C$ ．直线 $y = - \frac{1}{2} x - 2$ 经过点 $A$ ， $C$ ．

（1）求抛物线的解析式；

（2）点 $P$ 是抛物线上一动点，过点 $P$ 作 $x$ 轴的垂线，交直线 $AC$ 于点 $M$ ，设点 $P$ 的横坐标为 $m$ ．

①当 $ΔPCM$ 是直角三角形时，求点 $P$ 的坐标；

②作点 $B$ 关于点 $C$ 的对称点 $B^{'}$ ，则平面内存在直线 $l$ ，使点 $M$ ， $B$ ， $B'$ 到该直线的距离都相等．当点 $P$ 在 $y$ 轴右侧的抛物线上，且与点 $B$ 不重合时，请直接写出直线 $l : y = kx + b$ 的解析式． $(k$ ， $b$ 可用含 $m$ 的式子表示）

在 $ΔABC$ 中， $CA = CB$ ， $∠ ACB = α$ ．点 $P$ 是平面内不与点 $A$ ， $C$ 重合的任意一点．连接 $AP$ ，将线段 $AP$ 绕点 $P$ 逆时针旋转 $α$ 得到线段 $DP$ ，连接 $AD$ ， $BD$ ， $CP$ ．

（1）观察猜想

如图1，当 $α = 60 °$ 时， $\frac{BD}{CP}$ 的值是　　，直线 $BD$ 与直线 $CP$ 相交所成的较小角的度数是　　．

（2）类比探究

如图2，当 $α = 90 °$ 时，请写出 $\frac{BD}{CP}$ 的值及直线 $BD$ 与直线 $CP$ 相交所成的较小角的度数，并就图2的情形说明理由．

（3）解决问题

当 $α = 90 °$ 时，若点 $E$ ， $F$ 分别是 $CA$ ， $CB$ 的中点，点 $P$ 在直线 $EF$ 上，请直接写出点 $C$ ， $P$ ， $D$ 在同一直线上时 $\frac{AD}{CP}$ 的值．

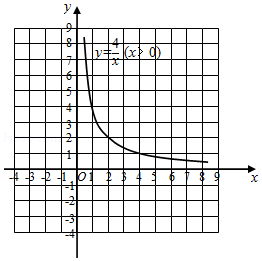
模具厂计划生产面积为4，周长为 $m$ 的矩形模具．对于 $m$ 的取值范围，小亮已经能用“代数”的方法解决，现在他又尝试从“图形”的角度进行探究，过程如下：

（1）建立函数模型

设矩形相邻两边的长分别为 $x$ ， $y$ ，由矩形的面积为4，得 $xy = 4$ ，即 $y = \frac{4}{x}$ ；由周长为 $m$ ，得 $2 (x + y) = m$ ，即 $y = - x + \frac{m}{2}$ ．满足要求的 $(x, y)$ 应是两个函数图象在第　一　象限内交点的坐标．

（2）画出函数图象

函数 $y = \frac{4}{x} (x > 0)$ 的图象如图所示，而函数 $y = - x + \frac{m}{2}$ 的图象可由直线 $y = - x$ 平移得到．请在同一直角坐标系中直接画出直线 $y = - x$ ．

（3）平移直线 $y = - x$ ，观察函数图象

①当直线平移到与函数 $y = \frac{4}{x} (x > 0)$ 的图象有唯一交点 $(2, 2)$ 时，周长 $m$ 的值为　　；

②在直线平移过程中，交点个数还有哪些情况？请写出交点个数及对应的周长 $m$ 的取值范围．

（4）得出结论

若能生产出面积为4的矩形模具，则周长 $m$ 的取值范围为　　．

学校计划为“我和我的祖国”演讲比赛购买奖品．已知购买3个 $A$ 奖品和2个 $B$ 奖品共需120元；购买5个 $A$ 奖品和4个 $B$ 奖品共需210元．

（1）求 $A$ ， $B$ 两种奖品的单价；

（2）学校准备购买 $A$ ， $B$ 两种奖品共30个，且 $A$ 奖品的数量不少于 $B$ 奖品数量的 $\frac{1}{3}$ ．请设计出最省钱的购买方案，并说明理由．