(本题10分)如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC =70°.
(1)求∠EDC的度数;
(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移, 使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
(本题10分)在平面直角坐标系xOy中, A、B两点分别在x轴、y轴的正半轴上,且OB = OA=3.
(1)求点A、B的坐标;(2)已知点C(-2,2),求△BOC的面积; (3)点P是第一象限角平分线上一点,若 ,求点P的坐标.
,求点P的坐标.
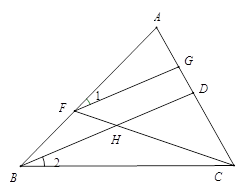
(本题6分)如图:BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H.∠GFH+∠BHC=180°,求证: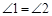 .
.
(本题6分)已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30°.
(1)求证:DC//AB.
(2)求∠AFE的大小.
(本题6分)已知直线AB和CD相交于点O,∠AOC为锐角,过O点作直线OE、OF.若OE⊥CD,OF平分∠AOE,求∠AOF+∠COF的度数.