模具厂计划生产面积为4,周长为的矩形模具.对于的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)建立函数模型
设矩形相邻两边的长分别为,,由矩形的面积为4,得,即;由周长为,得,即.满足要求的应是两个函数图象在第 一 象限内交点的坐标.
(2)画出函数图象
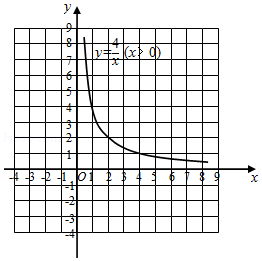
函数的图象如图所示,而函数的图象可由直线平移得到.请在同一直角坐标系中直接画出直线.
(3)平移直线,观察函数图象
①当直线平移到与函数的图象有唯一交点时,周长的值为 ;
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长的取值范围.
(4)得出结论
若能生产出面积为4的矩形模具,则周长的取值范围为 .
如图,在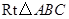 中,斜边
中,斜边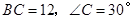 ,
, 为
为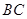 的中点,
的中点,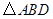 的外接圆
的外接圆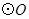 与
与 交于
交于 点,过
点,过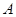 作
作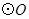 的切线
的切线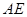 交
交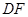 的延长线于
的延长线于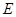 点.
点.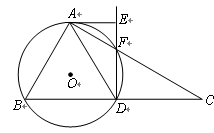
(1)求证: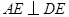 ;
;
(2)计算: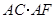 的值.
的值.
“六一”儿童节,小明与小亮受邀到科技馆担任义务讲解员,他们俩各自独立从A区(时代辉煌)、B区(科学启迪)、C区(智慧之光)、D区(儿童世界)这四个主题展区中随机选择一个为参观者服务.
(1)请用列表法或画树状图法说明当天小明与小亮出现在各主题展区担任义务讲解员的所有可能情况.(用字母表示)
(2)求小明与小亮只单独出现在B区(科学启迪)、C区(智慧之光)、D区(儿童世界)三个主题展区中担任义务讲解员的概率.
如图,在梯形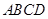 中,
中,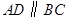 ,
,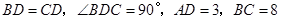 .求
.求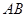 的长.
的长.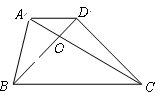
某县政府打算用25000元用于为某乡福利院购买每台价格为2000元的彩电和每台价格为1800元的冰箱,并计划恰好全部用完此款.
(1)问原计划所购买的彩电和冰箱各多少台?
(2)由于国家出台“家电下乡”惠农政策,该县政府购买的彩电和冰箱可获得13%的财政补贴,若在不增加县政府实际负担的情况下,能否多购买两台冰箱?谈谈你的想法.
芜湖市1985年~2008年各年度专利数一览表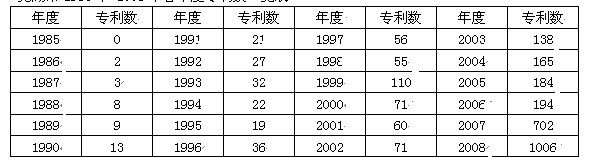
(1)请你根据以上专利数数据,求出该组数据的中位数为;极差为;
(2)请用折线图描述2001年~2008年各年度的专利数.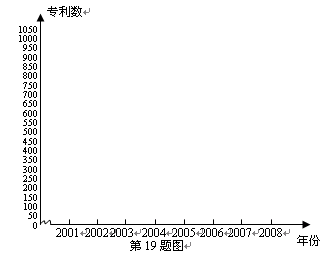
(3)请你根据这组数据,说出你得到的信息.