如图，在平面直角坐标系xOy中，已知直线PA是一次函数y=x＋m（m＞0）的图象，直线PB是一次函数y=－3x＋n（n＞m）的图象，点P是两直线的交点，点A、B、C、Q分别是两条直线与坐标轴的交点．
（1）用m、n分别表示点A、B、P的坐标及∠PAB的度数；
（2）若四边形PQOB的面积是4，且CQ：AO=2：1，试求点P的坐标，并求出直线PA与PB的函数表达式；
（3）在（2）的条件下，是否存在一点D，使以A、B、P、D为顶点的四边形是平行四边形？若存在，求出点D的坐标；若不存在，请说明理由．
（年湖南张家界12分）如图，在平面直角坐标系中，O为坐标原点，抛物线过
过O、B、C三点，B、C坐标分别为（10，0）和（
，
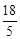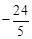），以OB为直径的⊙A经过C点,直线l垂直于x轴于点B.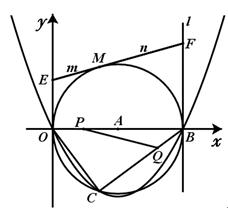
（1）求直线BC的解析；
（2）求抛物线解析式及顶点坐标；
（3）点M是⊙A上一动点（不同于O，B），过点M作⊙A的切线，交y轴于点E，交直线l于点F，设线段ME长为m ，MF长为n，请猜想
的值，并证明你的结论；
（4）点P从O出发，以每秒1个单位速度向点B作直线运动，点Q同时从B出发，以相同速度向点C作直线运动，经过t(0<t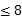
)秒时恰好使△BPQ为等腰三角形，请求出满足条件的t值.
（2014年湖南岳阳10分）数学活动﹣求重叠部分的面积
（1）问题情境：如图①，将顶角为120°的等腰三角形纸片（纸片足够大）的顶点P与等边△ABC的内心O重合，已知OA=2，则图中重叠部分△PAB的面积为 ．
（2）探究1：在（1）的条件下，将纸片绕P点旋转至如图②所示位置，纸片两边分别与AC，AB交于点E，F，图②中重叠部分的面积与图①重叠部分的面积是否相等？如果相等，请给予证明；如果不相等，请说明理由．
（3）探究2：如图③，若∠CAB=α（0°＜α＜90°），AD为∠CAB的角平分线，点P在射线AD上，且AP=2，以P为顶点的等腰三角形纸片（纸片足够大）与∠CAB的两边AC，AB分别交于点E、F，∠EPF=180°﹣α，求重叠部分的面积．（用α或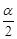
的三角函数值表示）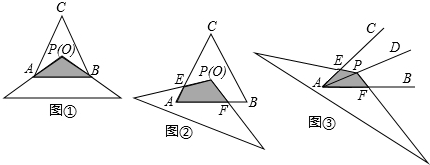
（年湖北黄石10分）如图，在矩形ABCD中，把点D沿AE对折，使点D落在OC上的F点，已知AO=8．AD=10．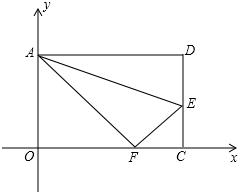
（1）求F点的坐标；
（2）如果一条不与抛物线对称轴平行的直线与该抛物线仅有一个交点，我们把这条直线称为抛物线的切线，已知抛物线经过点O，F，且直线y=6x﹣36是该抛物线的切线，求抛物线的解析式；
（3）直线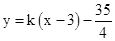
与（2）中的抛物线交于P、Q两点，点B的坐标为（3，
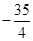），求证：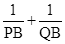
为定值．（参考公式：在平面直角坐标系中，若M（x1，y1），N（x2，y2），则M，N两点间的距离为|MN|=
）．
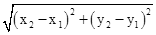（年湖北武汉12分）如图，已知直线AB：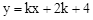
与抛物线
交于A、B两点，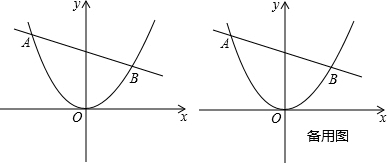
（1）直线AB总经过一个定点C，请直接写出点C坐标；
（2）当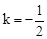
时，在直线AB下方的抛物线上求点P，使△ABP的面积等于5；
（3）若在抛物线上存在定点D使∠ADB＝90°，求点D到直线AB的最大距离.
（2014年湖北咸宁12分）如图，正方形OABC的边OA，OC在坐标轴上，点B的坐标为（﹣4，4）．点P从点A出发，以每秒1个单位长度的速度沿x轴向点O运动；点Q从点O同时出发，以相同的速度沿x轴的正方向运动，规定点P到达点O时，点Q也停止运动．连接BP，过P点作BP的垂线，与过点Q平行于y轴的直线l相交于点D．BD与y轴交于点E，连接PE．设点P运动的时间为t（s）．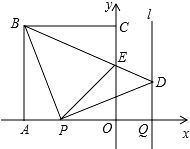
（1）∠PBD的度数为 ，点D的坐标为 （用t表示）；
（2）当t为何值时，△PBE为等腰三角形？
（3）探索△POE周长是否随时间t的变化而变化？若变化，说明理由；若不变，试求这个定值．