(年湖北黄石10分)如图,在矩形ABCD中,把点D沿AE对折,使点D落在OC上的F点,已知AO=8.AD=10.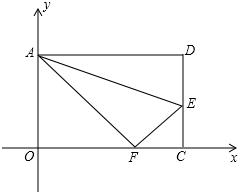
(1)求F点的坐标;
(2)如果一条不与抛物线对称轴平行的直线与该抛物线仅有一个交点,我们把这条直线称为抛物线的切线,已知抛物线经过点O,F,且直线y=6x﹣36是该抛物线的切线,求抛物线的解析式;
(3)直线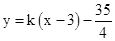 与(2)中的抛物线交于P、Q两点,点B的坐标为(3,
与(2)中的抛物线交于P、Q两点,点B的坐标为(3,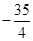 ),求证:
),求证: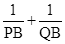 为定值.(参考公式:在平面直角坐标系中,若M(x1,y1),N(x2,y2),则M,N两点间的距离为|MN|=
为定值.(参考公式:在平面直角坐标系中,若M(x1,y1),N(x2,y2),则M,N两点间的距离为|MN|=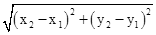 ).
).
如图,在离水面高度(AC)为2米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米的速度收绳子.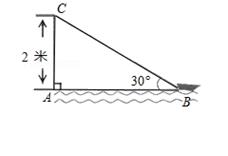
问:(1)未开始收绳子的时候,图中绳子BC的长度是多少米?
(2)收绳2秒后船离岸边多少米?(结果保留根号)
如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+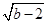 =0,过C作CB⊥x轴于B.
=0,过C作CB⊥x轴于B.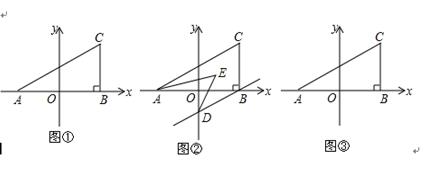
(1)求三角形ABC的面积.
(2)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图②,求∠AED的度数.
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过1000元后,超出1000元的部分按90%收费;在乙商场累计购物超过500元后,超出500元的部分按95%收费,设小红在同一商场累计购物x元,其中x>100.
(1)根据题题意,填写下表(单位:元)
累计购物 1300 2900 … x
在甲商场实际花费….
在乙商场实际花费..…
(2)当x取何值时,小红在甲、乙两商场的实际花费相同?
(3)当小红在同一商场累计购物超过1000元时,在哪家商场的实际花费少?
如图,已知∠1+∠2=180°,∠3=∠B,试猜想∠AED和∠C的关系,并证明你的结论.
为了解同学对体育活动的喜爱情况,某校设计了“你最喜欢的体育活动是哪一项(仅限一项)”的调查问卷.该校对本校学生进行随机抽样调查,以下是根据调查数据得到的统计图的一部分.请根据以上信息解答以下问题: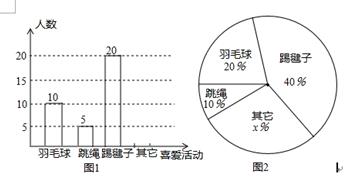
(1)该校对多少名学生进行了抽样调查?
(2)①请补全图1并标上数据 ②图2中x=.
(3)若该校共有学生900人,请你估计该校最喜欢跳绳项目的学生约有多少人?