甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过1000元后,超出1000元的部分按90%收费;在乙商场累计购物超过500元后,超出500元的部分按95%收费,设小红在同一商场累计购物x元,其中x>100.
(1)根据题题意,填写下表(单位:元)
累计购物 1300 2900 … x
在甲商场实际花费 ….
在乙商场实际花费 ..…
(2)当x取何值时,小红在甲、乙两商场的实际花费相同?
(3)当小红在同一商场累计购物超过1000元时,在哪家商场的实际花费少?
如图,在矩形ABCD中,AD=4,AB=m(m>4),点P是AB边上的任意一点(不与A、B重合),连结PD,过点P作PQ⊥PD,交直线BC于点Q.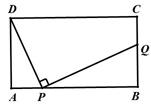
(1)当m=10时,是否存在点P使得点Q与点C重合?若存在,求出此时AP的长;若不存在,说明理由;
(2)连结AC,若PQ∥AC,求线段BQ的长(用含m的代数式表示)
(3)若△PQD为等腰三角形,求以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式,并写出m的取值范围.
如图,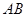 是
是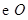 的直径,
的直径,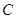 为圆周上一点,
为圆周上一点,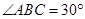 ,
,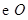 过点
过点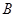 的切线与
的切线与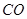 的延长线交于点
的延长线交于点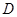 .
.
求证:(1)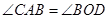 ;
;
(2)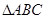 ≌
≌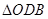 .
.
刘大叔去年承包了10亩地种植甲、乙两种蔬菜,共获利18000元,其中甲种蔬菜每亩获利2000元,乙种蔬菜每亩获利1500元,刘大叔去年甲、乙两种蔬菜各种植了多少亩?
先化简,再求值: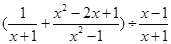 ,其中x=cos60°.
,其中x=cos60°.
设抛物线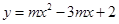 (
( )与x轴的交点为A(
)与x轴的交点为A( , 0),B(
, 0),B(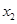 ,0),且
,0),且 ,其中
,其中 ,点P(a,b)为抛物线上一动点.
,点P(a,b)为抛物线上一动点.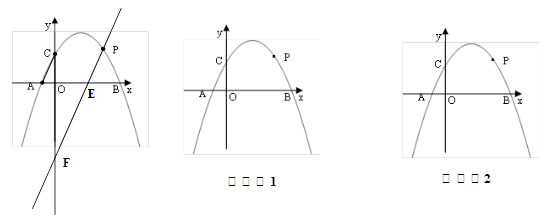
(1)求抛物线的解析式;
(2)连接AC,过P点做直线PE∥AC交x轴于点E,交y轴于点E(O,t),当a取何值时t有最大值,最大值是多少?
(3)判断在(2)的条件中是否存在一点P,使以点A、C、P、E为顶点的四边形为平行四边形.若不存在试说明理由;若存在,试求出点P的坐标.