某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓,清仓时单价为40元.设第二个月单价降低x元.
(1)填表:
| 时间 |
第一个月 |
第二个月 |
清仓 |
| 单价(元) |
80 |
|
40 |
| 销售量(件) |
200 |
|
|
(2)如果批发商希望通过销售这批T恤获利9 000元,那么第二个月的单价应是多少元?
(本题12分)如图,将一张正方形纸片剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.
(1)填表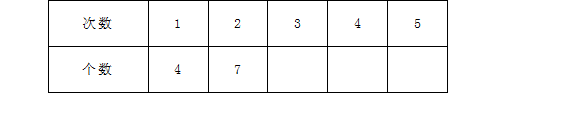
(2)如果剪了 次,共剪出多少个小正方形?
次,共剪出多少个小正方形?
(3)能否经过若干次分割后共得到2014片纸片?若能,请直接写出相应的次数,若不能,请说明理由.
(4)若将所给的正方形纸片剪成若干个小正方形(其大小可以不一样),那么你认为可以将它剪成六个小正方形吗?八个小正方形呢?如果可以,请在下图中画出剪割线的示意图;如果不可以,请简单说明理由.
(本题12分)如图,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形.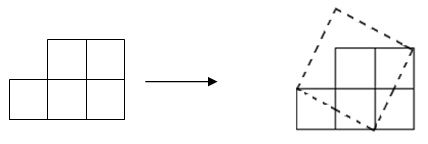
(1)拼成的正方形的面积与边长分别是多少?
(2)如图所示,以数轴的单位长度的线段为边作一个直角三角形,以数轴的-1点为圆心,直角三角形的最大边为半径画弧,交数轴正半轴于点A,那么点A表示的数是多少?点A表示的数的相反数是多少?
(3)你能把十个小正方形组成的图形纸,剪开并拼成正方形吗?若能,请画出示意图,并求它的边长是多少?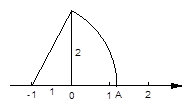
(本题10分)司机在驾驶汽车时,发现紧急情况到踩下刹车需要一段时间,这段时间叫反应时间,之后还会继续行驶一段距离.我们把司机从发现紧急情况到汽车停止所行驶的这段距离叫“刹车距离”(如图).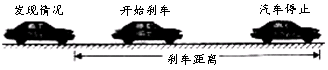
已知汽车的刹车距离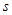 (单位:米)与车速
(单位:米)与车速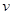 (单位:米/秒)之间有如下关系:
(单位:米/秒)之间有如下关系: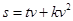 ,其中
,其中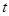 为司机的反应时间(单位:秒),
为司机的反应时间(单位:秒),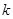 为制动系数.某机构为测试司机饮酒后刹车距离的变化,对某种型号的汽车进行了“醉汉”驾车测试,已知该型号汽车的制动系数
为制动系数.某机构为测试司机饮酒后刹车距离的变化,对某种型号的汽车进行了“醉汉”驾车测试,已知该型号汽车的制动系数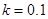 ,并测得志愿者在未饮酒时的反应时间
,并测得志愿者在未饮酒时的反应时间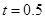 秒.
秒.
(1)若志愿者未饮酒,且车速为10米/秒,则该汽车的刹车距离为米 ;
(2)当志愿者在喝下一瓶啤酒半小时后,以15米/秒的速度驾车行驶,测得刹车距离为52.5米,此时该志愿者的反应时间是秒.
(3)假如该志愿者当初是以10米/秒的车速行驶,则刹车距离将比未饮酒时增加多少?
(本题10分)
“十·一”黄金周期间,人民公园在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)(单位:万人)
(1)若9月30日的游客人数记为a,请用a的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由;
(3)若9月30日的游客人数为2万人,门票每人10元,问黄金周期间人民公园门票收入是多少元?
(本题8分)为节约水资源,某初中环保宣传小组作了一个调查,得到了如下的一组数据:我们所在的城市大约有160万人,每天早晨起来漱口,如果大家都有一个坏习惯,漱口时都不关水龙头,那么我们每个人漱口时要浪费56毫升的水.
(1)按这样计算,我们全市一天早晨要浪费多少升水?请用科学计数法表示最后的结果,并精确到千位.
(2)如果我们用500毫升的纯净水瓶来装浪费的水,可以装多少瓶?