如图,矩形OABC在平面直角坐标系中,O为坐标原点,点A(0,4),C(2,0),将矩形OABC绕点O按顺时针方向旋转1350,得到矩形EFGH(点E与O重合).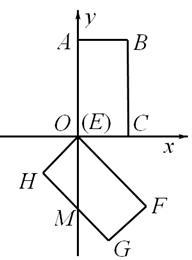
(1)若GH交y轴于点M,则∠FOM= ,OM= ;
(2)矩形EFGH沿y轴向上平移t个单位.
①直线GH与x轴交于点D,若AD∥BO,求t的值;
②若矩形EFHG与矩形OABC重叠部分的面积为S个平方单位,试求当0<t≤ 时,S与t之间的函数关系式.
时,S与t之间的函数关系式.
如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(﹣1,2),B(﹣3,4)C(﹣2,6)
(1)画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1
(2)以原点O为位似中心,画出将△A1B1C1三条边放大为原来的2倍后的△A2B2C2.
如示意图,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区,并将盲区内的那段公路计为BC.一辆以60km/h匀速行驶的汽车经过公路段的时间是3s,已知广告牌和公路的距离是40m,求小华家到公路的距离.(精确到1m)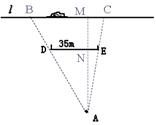
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B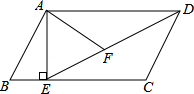
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6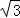 ,AF=4
,AF=4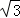 ,求AE的长.
,求AE的长.
网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,试说明△ABC∽△DEF.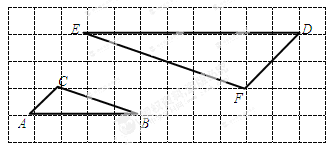
某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).
问:(1)当购买乒乓球多少盒时,两种优惠办法付款一样?
(2)当购买30盒乒乓球时,若让你选择一家商店去办这件事,你打算去哪家商店购 买?为什么?