(本题12分)如图,若点 在数轴上对应的数为
在数轴上对应的数为 ,点
,点 在数轴上对应的数为
在数轴上对应的数为 ,且
,且 ,
, 满足
满足 .点
.点 与点
与点 之间的距离表示为
之间的距离表示为 (以下类同).
(以下类同).
(1)求 的长;
的长;
(2)点 在数轴上对应的数为
在数轴上对应的数为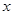 ,且
,且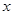 是方程
是方程 的解,在数轴上是否存在点
的解,在数轴上是否存在点 ,使得
,使得 ?若存在,求出点
?若存在,求出点 对应的数;若不存在,说明理由;
对应的数;若不存在,说明理由;
(3)在(1)、(2)的条件下,点 ,
, ,
, 开始在数轴上运动,若点
开始在数轴上运动,若点 以每秒
以每秒 个单位长度的速度向左运动,同时,点
个单位长度的速度向左运动,同时,点 和点
和点 分别以每秒
分别以每秒 个单位长度和
个单位长度和 个单位长度的速度向右运动,经过
个单位长度的速度向右运动,经过 秒后,请问:
秒后,请问: 的值是否随着时间
的值是否随着时间 的变化而改变?若变化,请说明理由;若不变,请求其常数值.
的变化而改变?若变化,请说明理由;若不变,请求其常数值.
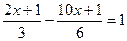 .
.
.用一副三角板,可以画出那些度数的角?
合并同类项: ,并求当x=2,y=1时,代数式的值.
,并求当x=2,y=1时,代数式的值.
(本小题满分6分)
端午节吃粽子是中华民族的传统习俗,五月初五早上,奶奶为小明准备了四只粽子:一
只 肉馅,一只香肠馅,两只红枣馅,四只粽子除内部馅料不同外其他均一切相同。小明喜欢
肉馅,一只香肠馅,两只红枣馅,四只粽子除内部馅料不同外其他均一切相同。小明喜欢
吃红枣馅的粽子。
(1)请你用树状图为小明预测一下吃两只粽子刚好都是红枣馅的概率;
(2)在吃粽子之前,小明准备用一格均匀的正四面体骰子(如图所示)
进行吃粽子的模拟试验,规定:掷得点数1向上代表肉馅,点数2向上代
表香肠馅,点数3, 向上代表红枣馅,连续抛掷这个骰子两次表示随机
向上代表红枣馅,连续抛掷这个骰子两次表示随机
吃两只粽子,从而估计吃两只粽子刚好都是红枣馅的概率。你认为这样模拟正确吗?试说明理由。
(本小题满分6分)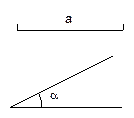
(1)画图,已知线段a和锐角 ,求作Rt△ABC,使它的一边为a,一锐角为
,求作Rt△ABC,使它的一边为a,一锐角为 (不写作法,要保留作图痕迹,作出其中一个满足条件的直角三角形即可)。
(不写作法,要保留作图痕迹,作出其中一个满足条件的直角三角形即可)。
(2)回答问题:
1满足上述条件的大小不同的共有种。
|
2若 =
= ,求最大的Rt△ABC的面积。
,求最大的Rt△ABC的面积。