如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△
，连结
、
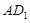．若∠ACB=30°，AB=2，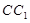
=x，四边形
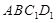的面积为S.
（1）线段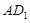的长度最小值是_____，此时x=" _____"
（2）当x为何时，四边形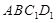是菱形？并说明理由；
(3)求S与x的函数关系式，并在直角坐标系中画出这个函数的图象
如图，在□ABCD中，点E是DC的中点，连接AE，并延长交BC的延长线于点F．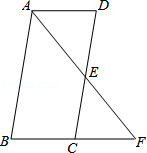
（1）求证：△ADE和△CEF的面积相等；
（2）若AB=2AD，试说明AF恰好是∠BAD的平分线．
（1）化简：
+
．
（2）解分式方程：
解不等式
﹣
≥1，并把它的解集在数轴上表示出来．
【背景知识】
数轴是初中数学的一个重要工具．利用数轴可以将数与形完美的结合．研究数轴我们发现了许多重要的规律：数轴上
点、
点表示的数为
、
，则，两点之间的距离
，若
，则可简化为
；线段
的中点
表示的数为
．
【问题情境】
已知数轴上有、两点，分别表示的数为
，
，点以每秒
个单位的速度沿数轴向右匀速运动，点以每秒
个单位向左匀速运动．设运动时间为
秒（
）．
【综合运用】
（1）运动开始前，、两点的距离为；线段的中点所表示的数．
（2）点运动秒后所在位置的点表示的数为；点运动秒后所在位置的点表示的数为；（用含的代数式表示）
（3）它们按上述方式运动，、两点经过多少秒会相遇，相遇点所表示的数是什么？
（4）若，按上述方式继续运动下去，线段的中点能否与原点重合，若能，求出运动时间，并直接写出中点的运动方向和运动速度；若不能，请说明理由．（当，两点重合，则中点也与， 两点重合）
为实现区域教育均衡发展，我区计划对
，
两类薄弱学校全部进行改造．已知改造一所类学校和两所类学校共需资金
万元；改造两所类学校和一所类学校共需资金
万元．问改造一所类学校和一所类学校分别需要多少万元的资金？
（1）老师让两位同学上黑板板演，其中甲同学设了一个未知数，请你帮他写出完整的解答过程．
（2）另一位乙同学设了两个未知数，却没法做下去，老师说也可以做，但需要列两个不同的方程，爱动脑的你能帮助她列出方程吗？
解：设改造一所类学校需要
万元资金；改造一所类学校需要
万元资金，根据题意可得
方程①：
方程②：
（3）丙同学说我一个未知数也没有设，也可以求出答案来．请聪明的你写出丙同学的方法．