为实现区域教育均衡发展,我区计划对 ,
, 两类薄弱学校全部进行改造.已知改造一所
两类薄弱学校全部进行改造.已知改造一所 类学校和两所
类学校和两所 类学校共需资金
类学校共需资金 万元;改造两所
万元;改造两所 类学校和一所
类学校和一所 类学校共需资金
类学校共需资金 万元.问改造一所
万元.问改造一所 类学校和一所
类学校和一所 类学校分别需要多少万元的资金?
类学校分别需要多少万元的资金?
(1)老师让两位同学上黑板板演,其中甲同学设了一个未知数,请你帮他写出完整的解答过程.
(2)另一位乙同学设了两个未知数,却没法做下去,老师说也可以做,但需要列两个不同的方程,爱动脑的你能帮助她列出方程吗?
解:设改造一所 类学校需要
类学校需要 万元资金;改造一所
万元资金;改造一所 类学校需要
类学校需要 万元资金,根据题意可得
万元资金,根据题意可得
方程①:
方程②:
(3)丙同学说我一个未知数也没有设,也可以求出答案来.请聪明的你写出丙同学的方法.
点P(x,y)在直线x+y=8上,且x>0,y>0,点A的坐标为(6,0),设△OPA的面积为S.
(1)求S与x的函数关系式,并直接写出x的取值范围;
(2)当S=12时,求点P的坐标.
已知▱ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD、AB于E、F,求证:AE=CF.
在平面直角坐标系中,直线y=kx-2经过点A(-2,0),求不等式4kx+3≤0的解集.
化简:
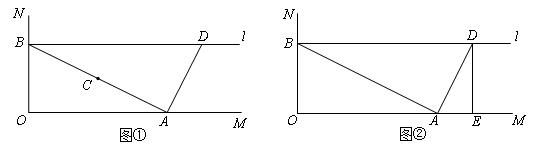
如图,∠MON=90°,A、B分别是OM、ON上的点,OB=4.点C是线段AB的中点,将线段AC以点A为旋转中心,沿顺时针方向旋转90°,得到线段AD,过点B作ON的垂线 .
.
(1)当点D恰好落在垂线 上时,求OA的长;
上时,求OA的长;
(2)过点D作DE⊥OM于点E,将(1)问中的△AOB以每秒2个单位的速度沿射线OM方向平移,记平移中的△AOB为△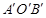 ,当点O′与点E重合时停止平移.设平移的时间为t秒,△
,当点O′与点E重合时停止平移.设平移的时间为t秒,△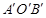 与△DAE重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围;
与△DAE重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围;
(3)在(2)问的平移过程中,若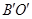 与线段
与线段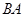 交于点P,连接
交于点P,连接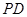 ,
, ,
, ,是否存在这样的t,使△
,是否存在这样的t,使△ 是等腰三角形?若存在,求出t的值;若不存在,请说明理由.
是等腰三角形?若存在,求出t的值;若不存在,请说明理由.