一学校为了绿化校园环境,向某园林公司购买力一批树苗,园林公司规定:如果购买树苗不超过60棵,每棵售价120元;如果购买树苗超过60棵,每增加1棵,所出售的这批树苗每棵售价均降低0.5元,但每棵树苗最低售价不得少于100元,该校最终向园林公司支付树苗款8800元,请问该校共购买了多少棵树苗?
(本题10分)在Rt△ABC中,∠CAB=90°,AB=AC.
(1)如图①,过点A在△ABC外作直线MN,BM⊥MN于M,CN⊥MN于N.
①判断线段MN、BM、CN之间有何数量关系,并证明;
②若AM= ,BM=
,BM= ,AB=
,AB= ,试利用图①验证勾股定理
,试利用图①验证勾股定理 ;
;
(2)如图②,过点A在△ABC内作直线MN,BM⊥MN于M,CN⊥MN于N,判断线段MN、BM、CN之间有何数量关系?(直接写出答案)
(本题6分)探索与应用.先填写下表,通过观察后再回答问题:
(1)表格中x=;y=;
(2)从表格中探究a与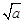 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知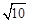 ≈3.16,则
≈3.16,则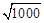 ≈;
≈;
②已知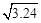 =1.8,若
=1.8,若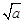 =180,则a=.
=180,则a=.
(本题8分)如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?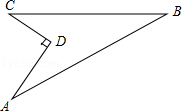
(本题8分)如图,△ABC中,∠BAC=110°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.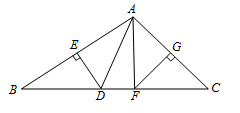
(1)求∠DAF的度数.
(2)如果BC=10,求△DAF的周长.
(本题7分)如图,点B、F、C、E在一条直线上,FB=CE,AC=DF,请从下列三个条件:①AB=DE;②∠A=∠D;③∠ACB=∠DFE中选择一个合适的条件,使AB∥ED成立,并给出证明.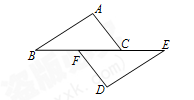
(1)选择的条件是(填序号)
(2)证明: