(本题10分)在Rt△ABC中,∠CAB=90°,AB=AC.
(1)如图①,过点A在△ABC外作直线MN,BM⊥MN于M,CN⊥MN于N.
①判断线段MN、BM、CN之间有何数量关系,并证明;
②若AM= ,BM=
,BM= ,AB=
,AB= ,试利用图①验证勾股定理
,试利用图①验证勾股定理 ;
;
(2)如图②,过点A在△ABC内作直线MN,BM⊥MN于M,CN⊥MN于N,判断线段MN、BM、CN之间有何数量关系?(直接写出答案)
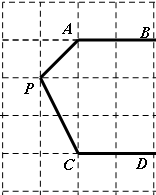
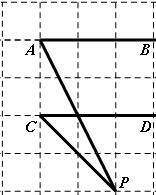
如图,在边长为 个单位长度的小正方形组成的网格中,已知
个单位长度的小正方形组成的网格中,已知 ,分别探讨下面三个图形中
,分别探讨下面三个图形中 与
与 、
、 的关系,请任选一个加以说明.(
的关系,请任选一个加以说明.( 分)
分)
( )(
)( )(
)( )
)
如图, 在平面直角坐标系中.
在平面直角坐标系中.
( )
) 点坐标是,
点坐标是, 点坐标是,
点坐标是, 点坐标是;(
点坐标是;( 分)
分)
( )把
)把 先向右平移
先向右平移 个单位,再向上平移
个单位,再向上平移 个单位,画出平移后的
个单位,画出平移后的 .(
.( 分)
分)
( )求
)求 的面积
的面积 .(
.( 分)
分)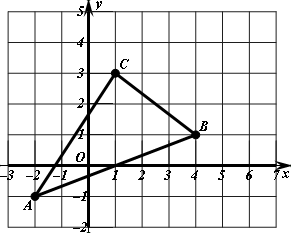
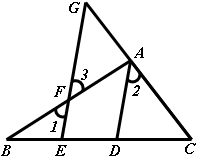
如图,已知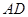 平分
平分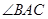 ,
,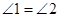 ,求证:
,求证: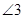
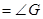 .(补全证明过程,每空
.(补全证明过程,每空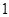 分,共
分,共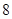 分)
分)
证明: 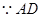 平分
平分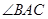 (已知 )
(已知 )
∴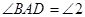 ( )
( )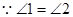 ()
()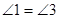 ()
()
∴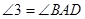 ( )
( )
∴ ( )
( )
∴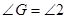 ()
()
∴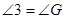 ()
()
如图,在边长为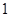 个单位长度的小正方形组成的网格中,小明家可用坐标
个单位长度的小正方形组成的网格中,小明家可用坐标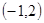 表示,汽车站可用坐标
表示,汽车站可用坐标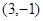 表示.
表示.
( )建立平面直角坐标系,画出
)建立平面直角坐标系,画出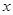 轴和
轴和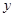 轴.(
轴.( 分)
分)
(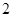 )某星期日早晨,小明同学从家出发,沿
)某星期日早晨,小明同学从家出发,沿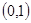
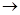
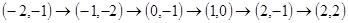 的路线转了一圈,又回到家里,写出他路上经过的地方;(
的路线转了一圈,又回到家里,写出他路上经过的地方;( 分)
分)
( )连接他在上一问中经过的地点,你得到了什么图形?(
)连接他在上一问中经过的地点,你得到了什么图形?( 分)
分)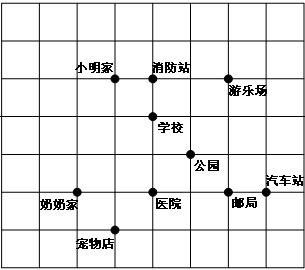
长江中下游地区特大旱情发生后,全国人民抗旱救灾,众志成城。市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
| 车型 |
甲 |
乙 |
丙 |
| 汽车运载量(吨/辆) |
5 |
8 |
10 |
| 汽车运费(元/辆) |
400 |
500 |
600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,温州市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?