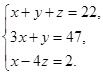（本题6分）探索与应用．先填写下表，通过观察后再回答问题：
（1）表格中x＝ ；y＝ ；
（2）从表格中探究a与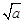
数位的规律，并利用这个规律解决下面两个问题：
①已知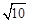
≈3.16，则
≈ ；
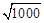②已知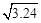
＝1.8，若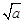＝180，则a＝ .
）解方程：（1）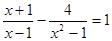
；（2）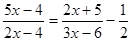
计算：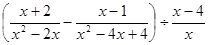
如图：点C在线段BD上，AB∥ED，∠A=∠1，∠E=∠2．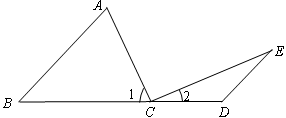
（1）若∠B=40°，求∠1、∠2的度数；
（2）判断AC与CE的位置关系，并说明理由．
上学期，我们学习了解一元一次方程及用一元一次方程解决实际问题．本学期，我们又学习了解二元一次方程组，试用二元一次方程组及以前解决实际问题的经验解决下列问题：
某校初一（1）班45名同学为“支援灾区”共捐款900元，捐款情况如下表：
| 捐款(元) |
5 |
10 |
20 |
50 |
| 人数 |
6 |
7 |
表中捐款10元和20元的人数不小心被墨水污染，看不清楚，请你确定表中的数据．
（1）解二元一次方程组：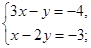
（2）试运用解二元一次方程组的思想方法，解三元一次方程组：