以下是根据全国人力资源和社会保障部公布的相关数据绘制的统计图的一部分,请你根据图中信息解答下列问题:

(1)2015年全国普通高校毕业生人数年增长率约是多少?(精确到0.1%)
(2)2013年全国普通高校毕业生人数约是多少万人?(精确到万位)
(3)补全折线统计图和条形统计图.
如图,矩形ABCD中,点O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC.
求证:(1)四边形EBFD是菱形; (2)MB : OE=3:2 .
一次函数 的图象经过A(0,﹣2),B(1,0)两点,与反比例函数
的图象经过A(0,﹣2),B(1,0)两点,与反比例函数 的图象在第一象限内的交点为M(m,4).
的图象在第一象限内的交点为M(m,4).
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.
A,B两个火车站相距360km.一列快车与一列普通列车分别从A,B两站同时出发相向而行,快车的速度比普通列车的速度快54km/h,当快车到达B站时,普通列车距离A站还有135km.求快车和普通列车的速度各是多少?
已知关于x的方程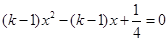 有两个相等的实数根,求实数k的值.
有两个相等的实数根,求实数k的值.