)解方程:(1)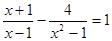 ;(2)
;(2)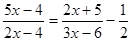
(本题满分12分)在平面直角坐标系中,抛物线交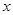 轴于
轴于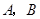 两点,交
两点,交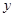 轴于点
轴于点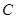 ,已知抛物线的对称轴为
,已知抛物线的对称轴为 .
.
 |
⑴求这个抛物线的解析式;
⑵在抛物线的对称轴上是否存在一点
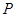 ,使点
,使点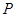 到A、C两点间的距离之和最大.若存在,求出点
到A、C两点间的距离之和最大.若存在,求出点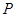 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(3)如果在
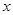 轴上方平行于
轴上方平行于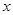 轴的一条直线交抛物线于
轴的一条直线交抛物线于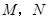 两点,以
两点,以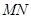 为直径作圆恰好与
为直径作圆恰好与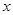 轴相切,求此圆的直径.
轴相切,求此圆的直径.
(本题满分12分)正方形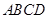 边长为4,
边长为4,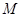 、
、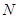 分别是
分别是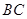 、
、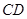 上的两个动点,当
上的两个动点,当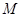 点在
点在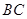 上运动时,保持
上运动时,保持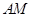 和
和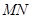 垂直,
垂直,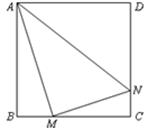
⑴证明:
 ;
;⑵设
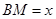 ,梯形
,梯形 的面积为
的面积为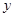 ,求
,求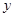 与
与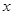 之间的函数关系式;
之间的函数关系式;⑶梯形
 的面积可能等于12吗?为什么?
的面积可能等于12吗?为什么?
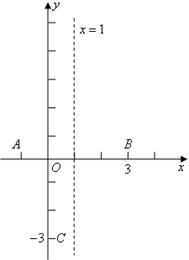
(本题满分10分)李经理到张家果园里一次性采购一种水果,他俩商定:李经理的采购价y(元/吨)与采购量x(吨)之间函数关系的图象如图中的折线段ABC所示(不包含端点A,但包含端点C).
⑴如果采购量x满足
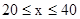 ,求y与x之间的函数关系式;
,求y与x之间的函数关系式;⑵已知张家种植水果的成本是2 800元/吨,李经理的采购量x满足
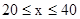 ,那么当采购量为多少时,张家在这次买卖中所获的利润w最大?最大利润是多少?
,那么当采购量为多少时,张家在这次买卖中所获的利润w最大?最大利润是多少?
(本题满分10分)用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为xm,窗户的透光面积为ym2,y与x的函数图象如图2所示.(图中顶点横坐标为1,纵坐标为1.5)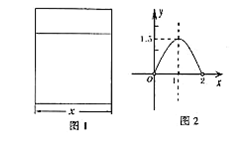
⑴写出y与x之间的函数关系式,指出当x为何值时,窗户透光面积最大?
⑵当窗户透光面积1.125m2时,窗框的两边长各是多少?
已知抛物线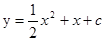 与x轴有两个不同的交点.
与x轴有两个不同的交点.(1) 求抛物线的对称轴;
(2) 求c的取值范围;
(3)若此抛物线与x轴两交点之间的距离为2,求c的值.