目前世界上最高的电视塔是广州新电视塔.如图8所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°,(sin39°≈0.63,cos39°≈0.78 , tan39°≈0.81)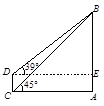
求大楼与电视塔之间的距离AC;
求大楼的高度CD(精确到1米)
(本题满分8分)如图,点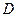 在
在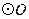 的直径
的直径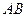 的延长线上,点
的延长线上,点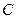 在
在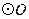 上,且AC=CD,∠ACD=120°.
上,且AC=CD,∠ACD=120°.
(1)求证: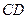 是
是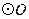 的切线;
的切线;
(2)若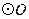 的半径为2,求图中阴影部分的面积.
的半径为2,求图中阴影部分的面积.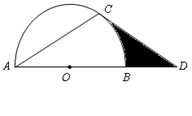
(本题满分8分)某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图 书角共30个.已知组建一个中型图书角需科
书角共30个.已知组建一个中型图书角需科 技类书籍80本,人文类书籍50本;组建一个小型图
技类书籍80本,人文类书籍50本;组建一个小型图 书角需科技类书籍30本,人文类书籍60本.
书角需科技类书籍30本,人文类书籍60本.
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
如图,在边长为1的小正方形组成的网格中,△ABC 的三个顶点均在格点上,请按要求完成下列各题:
的三个顶点均在格点上,请按要求完成下列各题:
(1)画线段AD∥BC且使AD =BC,连接CD;
(2)线段AC的长为,CD的长为,AD的长为;
(3)△ACD为三角形,四边形ABCD的面积为;
(4)若E为BC中点,则tan∠CAE的值是.
某生态示范园要对1号、2号、3号、4号四个新品种共500株果树幼苗进行成活实验,从中选出成活率高的品种进行推广.通过实验得知:3号果树幼苗成活率为89.6%,把实验数据绘制成下列两幅统计图(部分信息未给出).

(1)实验所用的2号果树幼苗的数量是_______株;
(2)求出3号果树幼苗的成活数,并把图2的统计图补充完整;
(3)你认为应选哪一种果树幼苗进行推广?请通过计算说明理由.
(本题满分8分)