已知:如图,两个长度为1的平面向量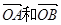 ,它们的夹角为
,它们的夹角为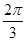 ,点C是以O为圆心的劣弧
,点C是以O为圆心的劣弧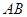 的中点. 求:(1)
的中点. 求:(1) 的值;(2)求
的值;(2)求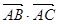 的值.
的值. 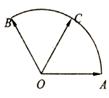
(本题12分)已知集合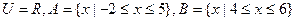 。
。
求:(1)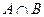 ;
;
(2)(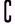
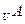 )
)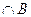
(3)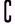
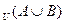
有n2(n≥4)个正数,排成n×n矩阵(n行n列的数表),其中每一行的数成等差数列,每一列的数 成等比数列,并且所有公比都相等,且满足a24=1,a42=
成等比数列,并且所有公比都相等,且满足a24=1,a42=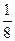 ,a43=
,a43= ,
,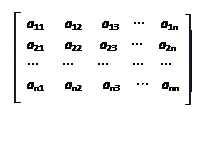
求:(1)公比q;
(2)用k表示a4k;
(3)求a11+a22+a33+…+ann的值。
△ABC中,AB= ,AC边上的中线BD=
,AC边上的中线BD= ,cosB=
,cosB= ,如图所示,
,如图所示, 求:sinA。
求:sinA。
已知,平面上三个向量 的模均为1,它们之间的夹角均为120°,
的模均为1,它们之间的夹角均为120°,
求:(1)证明 ;
;
(2) ,求k的取值范围。
,求k的取值范围。
已知数列{an}中, ,
,
求:(1)证明数列{bn}是等比数列;
(2)求数列{an}的通项公式。