已知,平面上三个向量 的模均为1,它们之间的夹角均为120°,
的模均为1,它们之间的夹角均为120°,
求:(1)证明 ;
;
(2) ,求k的取值范围。
,求k的取值范围。
已知 为第三象限角,
为第三象限角, .
.
(1)化简
(2)若 ,求
,求 的值(本小题满分10分)
的值(本小题满分10分)
从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:
⑴80~90这一组的频数、频率分别是多少?
⑵估计这次环保知识竞赛的及格率(60分及以上为及格). (本小题满分10分)
(1)已知 ,且
,且 为第三象限角,求
为第三象限角,求 的值
的值
(2)已知 ,计算
,计算 的值 (本小题满分10分)
的值 (本小题满分10分)
(本小题满分16分)已知函数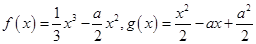 .
.
(1)当 时,求曲线
时,求曲线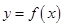 在点
在点 处的切线方程;
处的切线方程;
(2)当函数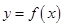 在区间
在区间 上的最小值为
上的最小值为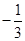 时,求实数
时,求实数 的值;
的值;
(3)当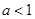 时,若函数
时,若函数 与
与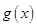 的图像有三个不同的交点,求实数
的图像有三个不同的交点,求实数 的取值范围.
的取值范围.
(小题满分14分)已知定义域为R的函数 是奇函数.
是奇函数.
(1)求 的值;
的值;
(2)若对任意的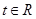 ,不等式
,不等式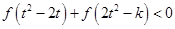 恒成立,求
恒成立,求 的取值范围.
的取值范围.