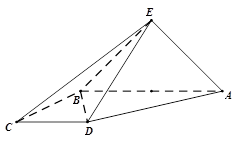
(本小题满分12分)如图,直角梯形 与等腰直角三角形
与等腰直角三角形 所在的平面互相垂直.
所在的平面互相垂直. ∥
∥ ,
, ,
, ,
, .
.
(1)求证: ;
;
(2)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)线段 上是否存在点
上是否存在点 ,使
,使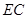 // 平面
// 平面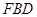 ?若存在,求出
?若存在,求出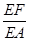 ;若不存在,说明理由.
;若不存在,说明理由.
已知函数f(x)=x(x+a)-lnx,其中a为常数.
(1)当a=-1时,求f(x)的极值;
(2)若f(x)是区间 内的单调函数,求实数a的取值范围;
内的单调函数,求实数a的取值范围;
(3)过坐标原点可以作几条直线与曲线y=f(x)相切?请说明理由.
设 是数列
是数列 的前
的前 项和,
项和,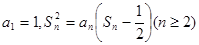 .
.
(1)求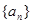 的通项;
的通项;
(2)设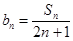 ,求数列
,求数列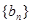 的前
的前 项和
项和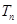 .
.
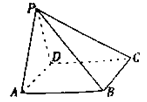
如图,四棱锥P-ABCD中,底面 为菱形,且
为菱形,且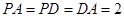 ,
, .
.
(1)求证: ;
;
(2)若 ,求二面角
,求二面角 的余弦值。
的余弦值。
已知函数 .
.
(1)设 ,且
,且 ,求θ的值;
,求θ的值;
(2)在△ABC中,AB=1, ,且△ABC的面积为
,且△ABC的面积为 ,求sinA+sinB的值.
,求sinA+sinB的值.
设函数f(x)=|2x﹣1|﹣|x+2|.
(Ⅰ)解不等式f(x)>0;
(Ⅱ)若∃x0∈R,使得f(x0)+2m2<4m,求实数m的取值范围.