设函数f（x）=|2x﹣1|﹣|x+2|．
（Ⅰ）解不等式f（x）＞0；
（Ⅱ）若∃x0∈R，使得f（x0）+2m2＜4m，求实数m的取值范围．
(本题满分12分)已知函数
在定义域
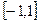上是奇函数，又是减函数。
（Ⅰ）证明：对任意的
，有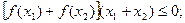
（Ⅱ）解不等式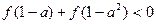
。
已知函数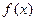
是在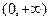
上每一点处均可导的函数，若
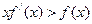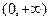在上恒成立。
（１）①求证：函数
在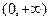上是增函数；
②当
时，证明：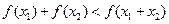
；
（２）已知不等式
在
且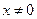
时恒成立，求证：
…
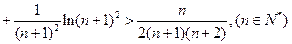
如图，在底面是直角梯形的四棱锥P—ABCD中，AD∥BC，∠DAB=90º，PA⊥平面ABCD，PA=AB=BC=1，AD=2，M是PD的中点。
（1）求证：MC∥平面PAB；
（2）在棱PD上求一点Q，使二面角Q—AC—D的正切值为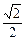
。
已知数列
、
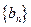满足：
，
，
。
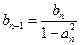（１）求数列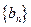的通项公式；
（２）若
，求数列｛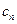
｝的前n项和
。
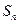已知函数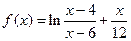
（１）求
的单调区间以及极值；
（２）函数
的图像是否为中心对称图形？如果是，请给出严格证明；如果不是，请说明理由。