（本小题满分12分）设函数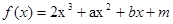
的导函数为
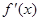，若函数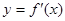
的图像关于直线
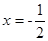对称，且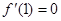
.
（1）求实数a、b的值
（2）若函数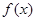
恰有三个零点，求实数
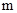的取值范围。
如图所示，已知空间四边形ABCD的各边和对角线的长都等于a，点M、N分别是AB、CD的中点.
（1）求证：MN⊥AB，MN⊥CD；
（2）求MN的长；
（3）求异面直线AN与CM所成角的余弦值.
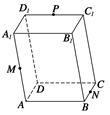
如图所示，在平行六面体ABCD-A1B1C1D1中，设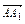
=a，
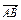=b，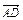
=c，M，N，P分别是AA1，BC，C1D1的中点，试用a，b，c表示以下各向量：
（1）
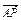；（2）
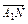；（3）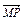
+
.
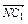）如图所示，平面ABEF⊥平面ABCD，四边形ABEF与ABCD都是直角梯
形，∠BAD=∠FAB=90°,BC
AD,BEFA,G、H分别为FA、FD的中点.
（1）证明：四边形BCHG是平行四边形；
（2）C、D、F、E四点是否共面？为什么？
（3）设AB=BE，证明：平面ADE⊥平面CDE.
如图所示，在三棱锥P—ABC中，PA⊥底面ABC，
（1）证明：平面PBE⊥平面PAC；
（2）如何在BC上找一点F，使AD∥平面PEF？并说明理由.
如图所示，ABCD是矩形，PA⊥平面ABCD，△PAD是等腰三角形，M、N分别是AB、PC的中点.求证：MN⊥平面PCD. 