)如图所示,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯 
形,∠BAD=∠FAB=90°,BC
 AD,BE
AD,BE
 FA,G、H分别为FA、FD的中点.
FA,G、H分别为FA、FD的中点.
(1)证明:四边形BCHG是平行四边形;
(2)C、D、F、E四点是否共面?为什么?
(3)设AB=BE,证明:平面ADE⊥平面CDE.
设
,
分别为椭圆
的左右焦点,过
的直线
与椭圆
相交于
,
两点,直线
的倾斜角为
,
到直线
的距离为
.
(Ⅰ)求椭圆
的焦距;
(Ⅱ)如果
,求椭圆
的方程。
为了比较注射
两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随即地分成两组。每组100只,其中一组注射药物
,另一组注射药物
.下表1和表2分别是注射药物A和药物B后的实验结果。(疱疹面积单位:
)
表1:注射药物
后皮肤疱疹面积的频数分布表

表2:注射药物 后皮肤疱疹面积的频数分布表

(Ⅰ)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;

(Ⅱ)完成下面
列联表,并回答能否有99.9%的把握认为"注射药物
后的疱疹面积与注射药物
后的疱疹面积有差异".
表3:


在
中,
分别为内角
的对边,且
.
(Ⅰ)求
的大小;
(Ⅱ)若
,是判断
的形状.
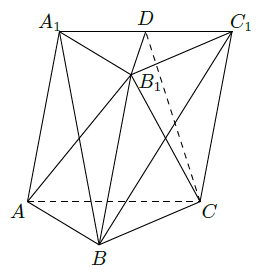
如图,棱柱
的侧面
是菱形,
.
(Ⅰ)证明:平面
平面
;
(Ⅱ)设
是
上的点,且
平面
,求
已知 、 、 均为正数,证明: ,并确定 、 、 为何值时,等号成立。