(本小题满分为14分)已知定义域为R的函数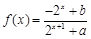 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
已知椭圆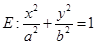 的右焦点为
的右焦点为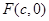 且
且 ,设短轴的一个端点为
,设短轴的一个端点为 ,原点
,原点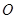 到直线
到直线 的距离为
的距离为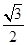 ,过原点和
,过原点和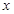 轴不重合的直线与椭圆
轴不重合的直线与椭圆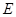 相交于
相交于 两点,且
两点,且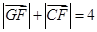 .
.
(1) 求椭圆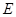 的方程;
的方程;
(2) 是否存在过点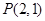 的直线
的直线 与椭圆
与椭圆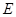 相交于不同的两点
相交于不同的两点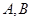 且使得
且使得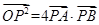 成立?若存在,试求出直线
成立?若存在,试求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
如图,在正三棱柱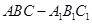 中,
中,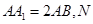 是
是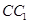 的中点,
的中点, 是线段
是线段 上的动点,且
上的动点,且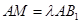
(1)若 ,求证:
,求证: ;
;
(2) 求二面角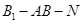 的余弦值;
的余弦值;
(3) 若直线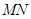 与平面
与平面 所成角的大小为
所成角的大小为 ,求
,求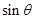 的最大值.
的最大值.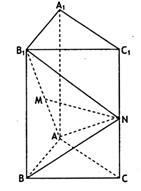
已知各项全不为零的数列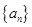 的前
的前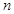 项和为
项和为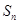 ,且
,且 ,
, 其中
其中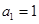
(1) 求数列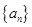 的通项公式;
的通项公式;
(2)在平面直角坐标系内,设点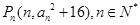 ,试求直线
,试求直线 斜率的最小值(
斜率的最小值( 为坐标原点).
为坐标原点).
某 单位为了提髙员工身体素质,特于近期举办了一场跳绳比赛
单位为了提髙员工身体素质,特于近期举办了一场跳绳比赛 ,其中
,其中 男员工12人,女员工18人,其成绩编成如右所示的茎叶图(单位:分).若分数在175分以上(含175分)者定为“运动健将”,并给
男员工12人,女员工18人,其成绩编成如右所示的茎叶图(单位:分).若分数在175分以上(含175分)者定为“运动健将”,并给 以特别奖励,其它人员则给予“运动积极分子”称号,同时又特别提议给女“运动健将”休假一天的待遇.
以特别奖励,其它人员则给予“运动积极分子”称号,同时又特别提议给女“运动健将”休假一天的待遇.
(1)若用分层抽样的方法从“运动健将”和“运动积极分子”中提取10人,然后再从这10人中 选4人,那么至少有1人是“运动健将”的概率是多少?
选4人,那么至少有1人是“运动健将”的概率是多少?
(2)若从所有“运动健将”中选3名代表,用 表示所选代表中女“运动健将”的人数,试写出
表示所选代表中女“运动健将”的人数,试写出 的分布列,并
的分布列,并 求
求 的数学期望.
的数学期望.
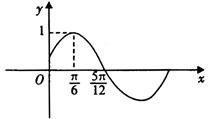
已知函数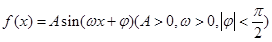 ,的部分图象如图所示.
,的部分图象如图所示.
(1) 求函数 的解析式;
的解析式;
(2) 如何由函数
 的图象通过适当的平移与伸缩变换得到函数
的图象通过适当的平移与伸缩变换得到函数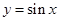 的图象,写出变换过程.
的图象,写出变换过程.