已知抛物线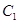 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线 :
: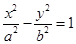 的左焦点
的左焦点 且垂直于
且垂直于 的两个焦点所在的轴,若抛物线
的两个焦点所在的轴,若抛物线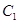 与双曲线
与双曲线 的一个交点是
的一个交点是 .
.
(1)求抛物线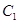 的方程及其焦点
的方程及其焦点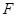 的坐标;
的坐标;
(2)求双曲线 的方程及其离心率
的方程及其离心率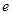 .
.
已知椭圆的两焦点是F1(0,-1),F2(0,1),离心率e=
(1)求椭圆方程;
(2)若P在椭圆上,且|PF1|-|PF2|=1,求cos∠F1PF2
在锐角 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
,
(1)求 的值;
的值;
(2)若 ,
, ,求
,求 的值.
的值.
设 是公比大于1的等比数列,
是公比大于1的等比数列, 为数列
为数列 的前
的前 项和.已知
项和.已知 ,且
,且 构成等差数列.
构成等差数列.
(1)求数列 的通项公式.
的通项公式.
(2)令 求数列
求数列 的前
的前 项和
项和 .
.
在正三棱柱ABC-A1B1C1中,若BB1=1,AB=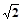 ,求AB1与C1B所成角的大小。
,求AB1与C1B所成角的大小。