已知数列
的前
项和
,且
的最大值为8.
(1)确定常数
,求
;
(2)求数列
的前
项和
.
设m是实数,记M={m|m>1},f(x)=log3(x2-4mx+4m2+m+ )
)
(1)证明: 当m∈M时,f(x)对所有实数都有意义;反之,若f(x)对所有实数x都有意义,则m∈M。
(2)当m∈M时,求函数f(x)的最小值。
(3)求证: 对每个m∈M,函数f(x)的最小值都不小于1。
设计一幅宣传画,要求画面面积为4840 cm2,画面的宽与高的比为λ(λ<1),画面的上、下各留8 cm的空白,左右各留5 cm空白,怎样确定画面的高与宽尺寸,才能使宣传画所用纸张面积最小?
如果要求λ∈[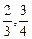 ],那么λ为何值时,能使宣传画所用纸张面积最小?
],那么λ为何值时,能使宣传画所用纸张面积最小?
设函数f(x)是定义在R上的偶函数,并在区间(-∞,0)内单调递增,f(2a2+a+1)<f(3a2-2a+1)。 求a的取值范围,并在该范围内求函数y=(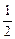 )
)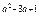 的单调递减区间.
的单调递减区间.
已知函数f(x)在(-1,1)上有定义,f(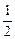 )=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(
)=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(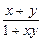 ),试证明:
),试证明:
(1)f(x)为奇函数;(2)f(x)在(-1,1)上单调递减.
已知函数f(x)= ,x∈[1,+∞
,x∈[1,+∞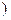
(1)当a=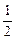 时,求函数f(x)的最小值。
时,求函数f(x)的最小值。
(2)若对任意x∈[1,+∞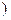 ,f(x)>0恒成立,试求实数a的取值范围。
,f(x)>0恒成立,试求实数a的取值范围。