在三棱柱
中,已知
,
,在
在底面
的投影是线段
的中点
。
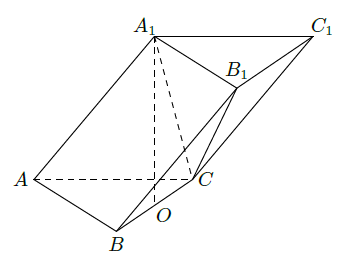
(1)证明在侧棱
上存在一点
,使得
平面
,并求出
的长;
(2)求平面
与平面
夹角的余弦值。
已知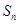 是等比数列
是等比数列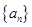 的公比
的公比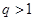 且
且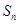 是它的前
是它的前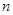 项的和。若
项的和。若 。(1)求数列
。(1)求数列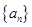 的通项公式;
的通项公式;
(2)设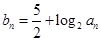 ,求数列
,求数列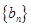 的前
的前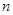 项和
项和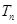 。
。
如图,△ABC中, ,点D 在BC边上,∠ADC=45°。
,点D 在BC边上,∠ADC=45°。
(1)求 的大小;(2)求AD的长。
的大小;(2)求AD的长。
在数列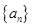 中,
中,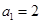 ,
, (
( ),数列
),数列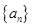 的前
的前 项和为
项和为 。(1)证明:数列
。(1)证明:数列 是等比数列,并求数列
是等比数列,并求数列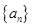 的通项公式;(2)求
的通项公式;(2)求 ;(3)证明:
;(3)证明: 。
。
在斜三角形 中,内角
中,内角 的对边分别为
的对边分别为 。若
。若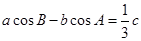 。(1)证明:
。(1)证明: ;(2)求
;(2)求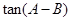 的最大值。
的最大值。
某厂生产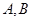 两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套
两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套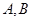 型会议桌需要加工木材的时间分别为1小时和2小时,上油漆需要的时间分别为3小时和1小时。厂里规定:加工木材的时间每天不得超过8小时,上油漆的时间每天不得超过9小时。已知该厂生产一套
型会议桌需要加工木材的时间分别为1小时和2小时,上油漆需要的时间分别为3小时和1小时。厂里规定:加工木材的时间每天不得超过8小时,上油漆的时间每天不得超过9小时。已知该厂生产一套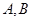 型会议桌分别可获得利润2千元和3千元,试问:该厂每天应分别生产
型会议桌分别可获得利润2千元和3千元,试问:该厂每天应分别生产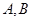 两型会议桌多少套,才能获得最大利润?最大利润是多少?
两型会议桌多少套,才能获得最大利润?最大利润是多少?