设函数 的图像关于直线 对称,其中 为常数,且 .
(1)求函数
的最小正周期;
(2)若
的图像经过点
,求函数
的值域。
已知等比数列{an}中,an > 0,公比q∈(0,1), 且a1a5+2a3a5+a2a8=25, a3与a5的等比中项为2.
(1)求数列{an}的通项公式;
(2)设bn=log2an,求数列{bn}的前n项和Sn.
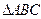 的面积是30,
的面积是30,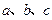 分别是三内角
分别是三内角 的对边,且
的对边,且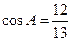 .
.
(1)求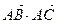 ; (2)若
; (2)若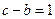 ,求
,求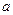 的值。
的值。
(本小题满分12分)已知函数 和点
和点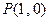 ,过点
,过点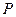 作曲线
作曲线 的两条切线
的两条切线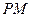 、
、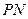 ,切点分别为
,切点分别为 、
、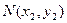 .
.
(1)求证: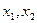 为关于
为关于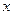 的方程
的方程 的两根;
的两根;
(2)设 ,求函数
,求函数 的表达式;
的表达式;
(3)在(2)的条件下,若在区间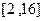 内总存在
内总存在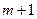 个实数
个实数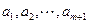 (可以相同),使得不等式
(可以相同),使得不等式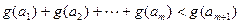 成立,求
成立,求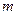 的最大值.
的最大值.
(本小题满分12分)设函数f(x)的定义域是R,对于任意实数m,n,恒有f(m+n)=f(m)f(n),且当x>0时,0<f(x)<1。
(1)求证:f(0)=1,且当x<0时,有f(x)>1;
(2)判断f(x)在R上的单调性;
⑶设集合A={(x,y)|f(x2)f(y2)>f(1)},集合B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B= ,求a的取值范围。
,求a的取值范围。
(本小题满分12分)已知向量
⑴ ;
;
⑵若