(本小题满分12分)设函数f(x)的定义域是R,对于任意实数m,n,恒有f(m+n)=f(m)f(n),且当x>0时,0<f(x)<1。
(1)求证:f(0)=1,且当x<0时,有f(x)>1;
(2)判断f(x)在R上的单调性;
⑶设集合A={(x,y)|f(x2)f(y2)>f(1)},集合B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B= ,求a的取值范围。
,求a的取值范围。
(本小题满分10分)
在平面直角坐标系xOy中,已知点 ,P是动点,且三角形POA的三边所在直线的斜
,P是动点,且三角形POA的三边所在直线的斜
率满足kOP+kOA=kPA.
(1)求点P的轨迹C的方程;
(2)若Q是轨迹C上异于点P的一个点,且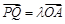 ,直线OP与QA交于点M,问:是否存在点P使得△PQA和△PAM的面积满足
,直线OP与QA交于点M,问:是否存在点P使得△PQA和△PAM的面积满足 ?若存在,求出点P的坐标;若不存在,说明理由.
?若存在,求出点P的坐标;若不存在,说明理由.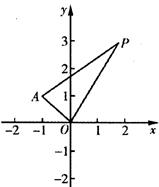
B选修4-4:坐标系与参数方程(本小题满分10分)
在直角坐标系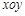 中,直线
中,直线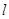 的参数方程为
的参数方程为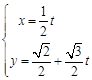 (
(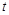 为参数),若以直角坐标系
为参数),若以直角坐标系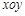 的
的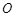 点为极点,
点为极点, 为极轴,且长度单位相同,建立极坐标系,得曲线
为极轴,且长度单位相同,建立极坐标系,得曲线 的极坐标方程为
的极坐标方程为 .
.
(1)求直线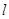 的倾斜角;
的倾斜角;
(2)若直线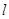 与曲线
与曲线 交于
交于 两点,求
两点,求 .
.
A选修4-2:矩阵与变换(本小题满分10分)
已知矩阵 ,向量
,向量 .求向量
.求向量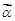 ,使得
,使得 .
.
(本小题满分16分)
已知函数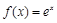 (其中
(其中 为自然对数的底数),
为自然对数的底数),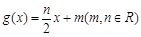 .
.
(1)若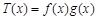 ,
, ,求
,求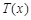 在
在 上的最大值;
上的最大值;
(2)若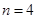 时方程
时方程 在
在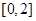 上恰有两个相异实根,求
上恰有两个相异实根,求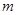 的取值范围;
的取值范围;
(3)若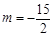 ,
,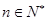 ,求使
,求使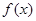 的图象恒在
的图象恒在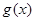 图象上方的最大正整数
图象上方的最大正整数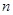 .
.
[注意: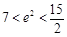 ]
]
(本小题满分16分)
已知数列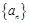 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为 ,
,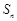 为其前
为其前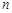 项和,且满足
项和,且满足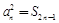 ,
,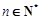 .数列
.数列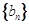 满足
满足 ,
,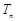 为数列
为数列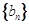 的前n项和.
的前n项和.
(1)求数列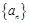 的通项公式
的通项公式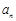 和数列
和数列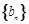 的前n项和
的前n项和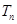 ;
;
(2)若对任意的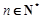 ,不等式
,不等式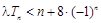 恒成立,求实数
恒成立,求实数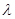 的取值范围;
的取值范围;
(3)是否存在正整数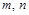
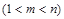 ,使得
,使得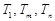 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有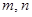 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.