已知等比数列
的公比为
.
(1)若
= ,求数列
的前
项和;
,求数列
的前
项和;
(Ⅱ)证明:对任意
,
,
,
成等差数列.
某企业为了适应市场需求,计划从2010年元月起,在每月固定投资5万元的基础上,元月份追加投资6万元,以后每月的追加投资额均为之前几个月投资额总和的20%,但每月追加部分最高限额为10万元. 记第n个月的投资额为

(1)求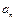 与n的关系式;
与n的关系式;
(2)预计2010年全年共需投资多少万元?(精确到0.01,参考数据: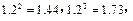

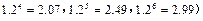

(本小题满分14分)设数列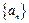 的前
的前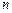 项和为
项和为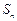 ,且
,且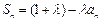 ,其中
,其中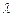 为常数,且
为常数,且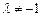 、0.(1)证明:数列
、0.(1)证明:数列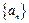 是等比数列;(2)设数列
是等比数列;(2)设数列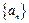 的公比
的公比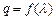 ,数列
,数列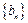 满足
满足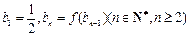 ,求数列
,求数列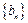 的通项公式;(3)设
的通项公式;(3)设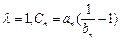 ,数列
,数列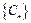 的前
的前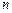 项和为
项和为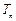 ,求证:当
,求证:当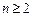 时,
时,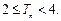
(本小题满分12分)已知二次函数 满足
满足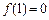 ,且关于
,且关于 的方程
的方程 的两个实数根分别在区间
的两个实数根分别在区间 、
、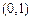 内.
内.
(1)求实数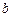 的取值范围;
的取值范围;
(2)若函数 在区间
在区间 上具有单调性,求实数
上具有单调性,求实数 的取值范围.
的取值范围.
(本小题满分14分)
已知数列 的前n项和为
的前n项和为 ,且
,且
(1)求数列 的通项公式;
的通项公式;
(2)设数列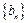 满足:
满足: ,且
,且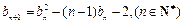 ,
,
求证: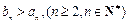 ;
;
(3)求证: 。
。
(本小题满分13分)已知函数 (其中x≥1)
(其中x≥1)
(1)求函数 的反函数
的反函数 ;
;
(2)设 ,求函数
,求函数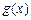 最小值及相应的x值;
最小值及相应的x值;
(3)若不等式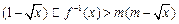 对于区间
对于区间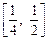 上的每一个x值都成立,求实数m的取值范围.
上的每一个x值都成立,求实数m的取值范围.