问题背景:
如图1，矩形铁片ABCD的长为2a，宽为a； 为了要让铁片能穿过直径为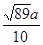
的圆孔，需对铁片进行处理（规定铁片与圆孔有接触时铁片不能穿过圆孔）；
探究发现:如图2，M、N、P、Q分别是AD、AB、BC、CD的中点，若将矩形铁片的四个角去掉，只余下四边形MNPQ，则此时铁片的形状是 _______，给出证明，并通过计算说明此时铁片都能穿过圆孔；
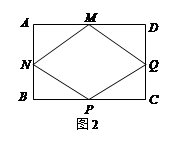
拓展迁移:如图3，过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F（不与端点重合），沿着这条直线将矩形 铁片切割成两个全等的直角梯形铁片；
①当BE=DF=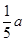
时，判断直角梯形铁片EBAF能否穿过圆孔，并说明理由；
②为了能使直角梯形铁片EBAF顺利穿过圆孔，请直接写出线段BE的长度的取值范围 ．
先化简，再求值：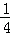
（4x2+2x﹣8）﹣（
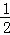x﹣1），其中x=．
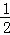当m为何值时，关于x的方程5m+3x=1+x的解比关于x的方程2x+m=3m的解大2？
解方程：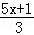
﹣
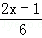=1．
化简：2（x2y+3xy2）﹣3（2xy2﹣4x2y）
已知数轴上的点A，B对应的数分别是x，y，且|x+100|+（y﹣200）2=0，点P为数轴上从原点出发的一个动点，速度为30单位长度/秒．
（1）求点A，B两点之间的距离；
（2）若点A向右运动，速度为10单位长度/秒，点B向左运动，速度为20单位长度/秒，点A，B和P三点同时开始运动，点P先向右运动，遇到点B后立即掉后向左运动，遇到点A再立即掉头向右运动，如此往返，当A，B两点相距30个单位长度时，点P立即停止运动，求此时点P移动的路程为多少个单位长度？
（3）若点A，B，P三个点都向右运动，点A，B的速度分别为10单位长度/秒，20单位长度/秒，点M、N分别是AP、OB的中点，设运动的时间为t（0＜t＜10），在运动过程中①
的值不变；②
的值不变，可以证明，只有一个结论是正确的，请你找出正确的结论并求值．