在四边形ABCD中,AD∥BC,且AD>BC,BC=6cm,P、Q分别从A、C
同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C出发向B运动,几
秒后四边形ABQP是平行四边形?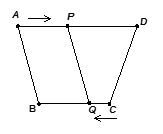
如图,在梯形ABCD中,AD∥BC,AB=AD+BC,E为CD的中点.
求证:AE⊥BE.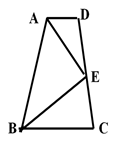
在平面直角坐标系中,分别描出点A(-1,0),B(0,2),C(1,0),
D(0,-2).
试判断四边形ABCD的形状;
若B、D两点不动,你能通过变动点A、C的位置使四边形ABCD成为正方形吗?若能,请写出变动后的点A、C的坐标.
如图,Rt△ABC中,∠C=90°,AC=BC,AB=4,试建立适当的直角
坐标系,并写出各顶点的坐标.
已知口ABCD中,M是边AB的中点,且BM=CM试说明四边形ABCD是矩形