某同学用图甲所示装置探究机械能守恒定律。水平桌面边缘带有最小分度为厘米的刻度，一辆小车通过不可伸长的细线跨过小滑轮与钩码相连。起初小车静止桌面右端，车的左端刚好与桌面上10.0cm处刻度对齐，钩码到地面的距离大于小车到滑轮的距离。启动频闪摄影系统后，释放钩码，小车在钩码的牵引下，由静止开始沿水平桌面运动，图乙是实验中得到的频闪照片的一部分。已知小车质量M =200g，钩码质量m=50g，闪光频率f=10.0Hz，重力加速度g=9.80m/s2。
乙
⑴用x表示小车从静止起运动到A点过程中通过的位移，vA表示小车运动至A点时的速度，若在误差允许的范围内，有公式 成立(用题中所给字母表示)，就可说明在此过程中由小车和钩码组成的系统机械能守恒。
⑵由频闪照片上的数据，可得小车到达A位置时系统的动能EK = J，小车从静止开始运动到A位置的过程中，钩码减少的重力势能Ep= J。(结果均保留三位有效数字）
⑶实验操作及测量均正确，经反复实验，数据几无变化。说明在此运动过程中系统机械能
（填“守恒”或“不守恒”），得此实验结果的主要原因应是 。
在“研究平抛物体的运动”实验中，某同学设计了如图所示的实验装置。他将斜槽AB固定在桌边，使槽的末端点的切线水平。将一斜面BC连接在斜槽末端，并在斜面上卡好纸带和复写纸。已知C端恰好与B的投影D位于同一水平面上。让小钢球几次都从斜槽顶端A处由静止开始滚下，球从B处飞出后落在斜面上，在纸带上留下几个落点位置。该同学画出一个小圆将落点都圈在其中，并取小圆的圆心位置作为小钢球的平均落点位置，如下图所示，其中折痕B为抛出点。
根据图中数据可知小球做平抛运动的位移大小x＝cm。
经测量B、D两点间距离H为30.00cm，斜面BC长L为50.00cm。当地重力加速度g＝9.80m/s2。根据该同学所采用的实验方法，请你写出小球在B处的平抛初速度v0的表达式（用题中所提及的物理量符号x、H、L、g表示）。
一水平放置的圆盘绕竖直固定轴转动,在圆盘上沿半径开有一条宽度为2 mm的均匀狭缝。将激光器与传感器上下对准,使二者间连线与转轴平行,分别置于圆盘的上下两侧,且可以同步地沿圆盘半径方向匀速移动,激光器连续向下发射激光束.在圆盘转动过程中,当狭缝经过激光器与传感器之间时,传感器接收到一个激光信号,并将其输入计算机,经处理后画出相应图线。图 (a)为该装置示意图,图(b)为所接收的光信号随时间变化的图线,横坐标表示时间,纵坐标表示接收到的激光信号强度,图中Δt1=1.0×10-3 s, Δt2=0.8×10-3 s.
利用图(b)中的数据可以知道1 s时圆盘转动的角速度rad/s；激光器和传感器沿半径移动的方向是（填“沿半径向圆心”或“沿半径向外”），移动的速度大小是m/s；还可以知道第三个激光信号的宽度Δt3= s 。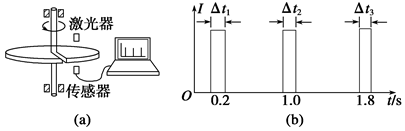
相距为L=2m、质量均为
的两小物块A、B，静止放在足够长的水平面上，它们与水平面间的动摩擦因数均为μ=0.2．现在用一个F=0.3mg的水平向右的恒力推A，A开始向右运动，并与B发生多次弹性碰撞，且每次碰撞时间极短，取g=10m∕s2。求：
（1）第一次碰撞后B的速度大小；
（2）第五次碰撞后至第六次碰撞前B的运动时间；
（3）B运动的总路程．
如图所示，在直角坐标系O-xyz中存在磁感应强度为
、方向竖直向下的匀强磁场，在（0，0，h）处固定一电量为+q（q>0）的点电荷，在xOy平面内有一质量为m(m未知),电量为-q的微粒绕原点O沿图示方向作匀速圆周运动。若微粒的圆周运动可以等效为环形电流，求：
（1）若已知+q与-q的连线与z轴的夹角θ和静电力常量k,则此微粒所受的库仑力多大
（2）此微粒作匀速圆周运动的角速度ω；
（3）等效环形电流的电流强度I（已知重力加速度为g）。
如图所示，水平放置的平行板电容器，原来两板不带电，上极板接地，它的极板长 L= 0.1m，两板间距离d =" 0.4" cm，有一束相同的带电微粒以相同的初速度先后从两板中央平行极板射入，由于重力作用微粒能落到下板上，微粒所带电荷立即转移到下极板且均匀分布在下极板上．设前一微粒落到下极板上时后一微粒才能开始射入两极板间。已知微粒质量为 m = 2×10-6kg，电量q = 1×10-8 C，电容器电容为C=10-6 F，取g=10m∕s2．求：
（1）第一个微粒运动的时间
（2）为使第一个微粒的落点范围能在下板中点B到紧靠右边缘的C点之内，求微粒入射的初速度v0的取值范围；
（3）若带电微粒均以第一问中初速度v0的最小值入射，求最后一个带电微粒落到下极板上时的电势能（取地面为零势能面）。