节水喷灌系统已经在我国很多地区使用。某节水喷灌系统如图所示，喷口距离地面的高度
，能沿水平方向旋转，水可沿水平方向喷出，喷水的最大速率
，每秒喷出水的质量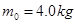
。所用的水是从井下抽取的，井中水面离地面的高度
，并一直保持不变。水泵由电动机带动，电动机电枢线圈电阻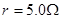
。电动机正常工作时，电动机的输入电压
，输入电流
。不计电动机的摩擦损耗，电动机的输出功率等于水泵所需要的最大输入功率。水泵的输出功率与输入功率之比称为水泵的抽水效率。
（计算时
可取3，球体表面积公式
）
（1）求这个喷灌系统所能喷灌的最大面积
；
（2）假设系统总是以最大喷水速度工作，求水泵的抽水效率
；
（3）假设系统总是以最大喷水速度工作，在某地区需要用蓄电池将太阳能电池产生的电能存储起来供该系统使用，根据以下数据求所需太阳能电池板的最小面积
。
已知：太阳光传播到达地面的过程中大约有
％的能量损耗，太阳辐射的总功率
，太阳到地球的距离
，太阳能电池的能量转化效率约为
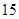％，蓄电池释放电能的效率约为
％。
公路上行驶的两汽车之间保持一定的安全距离。当前车突然停止时，后车司机可以采取刹车措施，使汽车在安全距离内停下而不会与前车相碰。通常情况下，人的反应时间和汽车系统的反应时间之和为1s。当汽车在晴天干燥沥青路面上以108km/h的速度匀速行驶时，安全距离为120m，设雨天时汽车轮胎与沥青路面间的动摩擦因数为晴天时的2/5，若要求安全距离仍为120m，求汽车在雨天安全行驶的最大速度。
如图所示，斜面倾角为
，一质量为
的木块恰能沿斜面匀速下滑，若用一水平恒力F作用于木块上，使之沿斜面向上做匀速运动，求此恒力F的大小。（
）
如图所示，一轻质弹簧上端悬挂于天花板，下端系一质量为m1=2.0kg的物体A，平衡时物体A距天花板h1=0.60m。在距物体A正上方高为h=0.45m处有一个质量为m2="1." 0kg的物体B,由静止释放B，下落过程某时刻与弹簧下端的物体A碰撞（碰撞时间极短）并立即以相同的速度运动。已知两物体不粘连，且可视为质点。g=l0m/s2。求：
(i)碰撞结束瞬间两物体的速度大小；
(ii)碰撞结束后两物体一起向下运动，历时0.25s第一次到达最低点。求在该过程中，两物体间的平均作用力。
直角等腰玻璃三棱镜ABC的截面如图所示， ABC= ACB=45°，一条单色光从腰AB上的D点射入三棱镜，在玻璃内部折射光线为DE，折射角r="30" ,折射光线传播到BC边上的E点。已知该玻璃砖的折射率n=
。
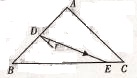
(i)求光线的入射角i（图中未标出）
(ii)判断光线能否在E点发生全反射。
）（如图所示，水平放置一个长方体气缸，总体积为V，用无摩擦活塞（活塞绝热、体积不计）将内部封闭的理想气体分为完全相同的A、B两部分。初始时两部分气体压强均为P，温度均为T。若使A气体的温度升高
，B气体的温度保持不变，求
(i)A气体的体积变为多少?
(ii)B气体在该过程中是放热还是吸热？