汽车额定功率为100kW,质量为5×103kg,设阻力恒为车重的0.1倍。(g=10m/s2)
(1)若汽车保持额定功率运动,求其达到的最大速度;
(2)若汽车以a=0.5m/s2的加速度匀加速运动,求其匀加速运动的最长时间.
一种红宝石激光器发射的激光是不连续的一道道闪光,每道闪光称为一个光脉冲,若这种激光器光脉冲的持续时间为1.0×10-11 s,波长为694.3 nm,发射功率为1.0×1010 W.
(1)每列光脉冲的长度是多少?
(2)用红宝石激光照射皮肤色斑,每1 cm2吸收能量达到60 J以后,色斑便逐渐消失,一颗色斑的面积是50 mm2,则它需要吸收多少个红宝石激光脉冲才能逐渐消失?
某脉冲激光器的耗电功率为2×103 W,每秒钟输出10个光脉冲,每个脉冲持续的时间为10-8 s,携带的能量为0.2 J.该激光器将电能转化为激光能量的效率为多少?
如图所示,水平地面上静止放置着物块B和C,相距L="1.0m" 。物块A以速度v0=10m/s沿水平方向与B正碰。碰撞后A和B牢固地粘在一起向右运动,并再与C发生正碰,碰后瞬间C的速度v=2.0m/s。已知A和B的质量均为m,C的质量为A质量的k倍,物块与地面的动摩擦因数μ=0.45。(设碰撞时间很短,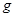 取10m/s2)⑴计算与C碰撞前瞬间AB的速度;⑵根据AB与C的碰撞过程分析k的取值范围,并讨论与C碰撞后AB的可能运动方向。
取10m/s2)⑴计算与C碰撞前瞬间AB的速度;⑵根据AB与C的碰撞过程分析k的取值范围,并讨论与C碰撞后AB的可能运动方向。
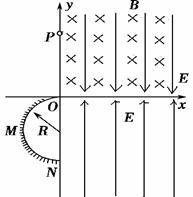
(18分)如下图,竖直平面坐标系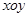 的第一象限,有垂直
的第一象限,有垂直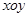 面向里的水平匀强磁场和竖直向下的匀强电场,大小分别为B和E;第四象限有竖直向上的匀强电场,大小也为
面向里的水平匀强磁场和竖直向下的匀强电场,大小分别为B和E;第四象限有竖直向上的匀强电场,大小也为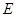 ;第三象限内有一绝缘光滑竖直放置的半径为
;第三象限内有一绝缘光滑竖直放置的半径为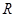 的半圆轨道,轨道最高点与坐标原点
的半圆轨道,轨道最高点与坐标原点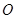 相切,最低点与绝缘光滑水平面相切于
相切,最低点与绝缘光滑水平面相切于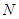 .一质量为
.一质量为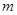 的带电小球从
的带电小球从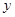 轴上(
轴上( )的
)的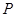 点沿
点沿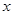 轴正方向进入第一象限后做匀速圆周运动,恰好通过坐标原点
轴正方向进入第一象限后做匀速圆周运动,恰好通过坐标原点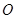 ,且水平切入半圆轨道并沿轨道内侧运动,过
,且水平切入半圆轨道并沿轨道内侧运动,过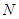 点水平进入第四象限,并在电场中运动(已知重力加速度为
点水平进入第四象限,并在电场中运动(已知重力加速度为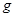 ).
).
(1)判断小球的带电性质并求出其所带电荷量;
(2)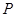 点距坐标原点
点距坐标原点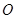 至少多高;
至少多高;
(3)若该小球以满足(2)中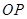 最小值的位置和对应速度进
最小值的位置和对应速度进
入第一象限,通过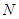 点开始计时,经时间
点开始计时,经时间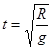 小球
小球
距坐标原点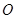 的距离
的距离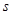 为多远?
为多远?
质量为0.2 kg的弹性球从空中某高度由静止开始下落,该下落过程对应的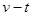 图象如图所示。球与水平地面相碰后离开地面时的速度大小为碰撞前的3/4。该球受到的空气阻力大小恒为
图象如图所示。球与水平地面相碰后离开地面时的速度大小为碰撞前的3/4。该球受到的空气阻力大小恒为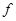 ,取
,取 ="10" m/s2, 求:
="10" m/s2, 求: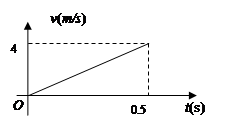
(1)弹性球受到的空气阻力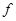 的大小;
的大小;
(2)弹性球第一次碰撞后反弹的最高点与弹性球从空中第一次静止下落位置的高度差Δh。