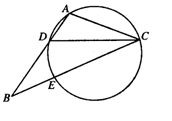
如图,在 中,
中,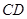 是
是 的角平分线,
的角平分线,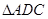 的外接圆交
的外接圆交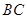 于点
于点 ,
,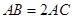 .
.
(Ⅰ)求证: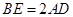 ;
;
(Ⅱ)当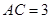 ,
,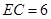 时,求
时,求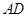 的长.
的长.
(本小题满分12分)已知函数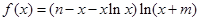 (
(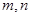 为常数,且
为常数,且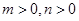 ),且曲线
),且曲线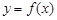 在点
在点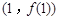 处的切线方程为
处的切线方程为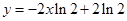 .
.
(Ⅰ)求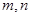 的值;
的值;
(Ⅱ)证明:对任意 ,曲线
,曲线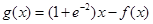 的图象在第一象限.
的图象在第一象限.
已知圆 的圆心在坐标原点
的圆心在坐标原点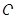 ,且恰好与直线
,且恰好与直线 相切,设点A为圆上一动点,
相切,设点A为圆上一动点, 轴于点
轴于点 ,且动点
,且动点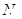 满足
满足 ,设动点
,设动点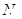 的轨迹为曲线
的轨迹为曲线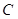
(Ⅰ)求曲线C的方程;
(Ⅱ)直线 交曲线
交曲线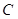 于不同的
于不同的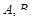 两点,
两点,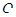 是坐标原点,求
是坐标原点,求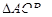 面积的最大值.
面积的最大值.
(本小题满分12分)已知在四棱锥 中,底面
中,底面 是菱形,且
是菱形,且 ,侧面
,侧面 是正三角形,且面
是正三角形,且面 面
面 ,
, 为
为 的中点.
的中点. 
(Ⅰ)证明: ∥面
∥面 ;
;
(Ⅱ)求面 与面
与面 所成二面角的余弦值.
所成二面角的余弦值.
(本小题满分12分)为了参加中央电视台、国家语言文字工作委员会联合主办的《中国汉字听写大会》节目,某老师要求参赛学生从星期一到星期四每天学习3个汉字以及正确注释,每周五对一周内所学汉字随机抽取若干个进行检测(一周所学的汉字每个被抽到的可能性相同).
(Ⅰ)老师随机抽了4个汉字进行检测,求至少有3个是后两天学习过的汉字的概率;
(Ⅱ)某学生对后两天所学过的汉字每个能默写对的概率为 ,对前两天所学过的汉字每个能默写对的概率为
,对前两天所学过的汉字每个能默写对的概率为 .若老师从后三天所学汉字中各抽取一个进行检测,求该学生能默写对的汉字的个数ξ的分布列和期望.
.若老师从后三天所学汉字中各抽取一个进行检测,求该学生能默写对的汉字的个数ξ的分布列和期望.