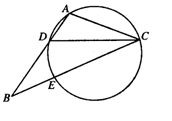
如图,在 中,
中,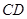 是
是 的角平分线,
的角平分线,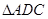 的外接圆交
的外接圆交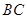 于点
于点 ,
,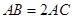 .
.
(Ⅰ)求证: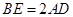 ;
;
(Ⅱ)当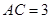 ,
,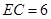 时,求
时,求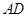 的长.
的长.
(本小题满分13分)
某零售店近五个月的销售额和利润额资料如下表:
| 商店名称 |
A |
B |
C |
D |
E E |
销售额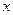 (千万元) (千万元) |
3 |
5 |
6 |
7 |
9 9 |
利润额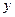 (百万元) (百万元) |
2 |
3 |
3 |
4 |
5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的 相关关系;
相关关系;
(2)用最小二乘法计算利润额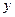 关于销售额
关于销售额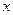 的回归直线方程;
的回归直线方程;
(3)当销售额为4(千万元)时,利用(2)的结论估计该零售店的利润额(百万元).
已知 是函数
是函数 的一个极值点,其中
的一个极值点,其中 ,
, .
.
(1)求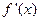 并求
并求 与
与 的关系式;
的关系式;
(2)当 时,求方程
时,求方程
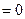 的实根个数;
的实根个数;
(3)当 时,函数
时,函数 的图象上任意一点的切线的斜率恒大于
的图象上任意一点的切线的斜率恒大于 ,求
,求 的取值范围.
的取值范围.
函数 对任意实数
对任意实数 都有
都有 .
.
(1)求 的值;
的值;
(2)若 ,求
,求 的值,猜想
的值,猜想 时
时 的表达式,并用数学归纳法证明你的结论.
的表达式,并用数学归纳法证明你的结论.
某突发事件,在不采取任何预防措施的情况下发生的概率为 ,一旦发生,将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择,单独采用甲、乙预防措施所需的费用分别为40万元和20万元,采用相应预防措施后此突发事件不发生的概率分别为
,一旦发生,将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择,单独采用甲、乙预防措施所需的费用分别为40万元和20万元,采用相应预防措施后此突发事件不发生的概率分别为 和
和 .若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用,请分别计算这几种预防方案的总费用,并指出哪一种预防方案总费用最少.
.若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用,请分别计算这几种预防方案的总费用,并指出哪一种预防方案总费用最少.
(注:总费用 = 采取预防措施的费用+发生突发事件损失的期望值)
随机变量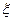 的分布列如下表所示:
的分布列如下表所示:
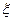 |
2 |
3 |
4 |
 |
 |
 |
 |
(1)求 的值以及
的值以及 ;
;
(2)求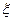 的数学期望
的数学期望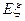 .
.