(本小题满分12分)设 到定点
到定点 的距离和它到直线
的距离和它到直线 距离的比是
距离的比是 .
.
(Ⅰ)求点 的轨迹方程;
的轨迹方程;
(Ⅱ) 为坐标原点,斜率为
为坐标原点,斜率为 的直线过
的直线过 点,且与点
点,且与点 的轨迹交于点
的轨迹交于点 ,
, ,若
,若 ,求△
,求△ 的面积.
的面积.
已知椭圆C的离心率为 ,直线
,直线 被以椭圆的短轴为直径的圆截得弦长为
被以椭圆的短轴为直径的圆截得弦长为 ,抛物线
,抛物线 以原点为顶点,椭圆的右焦点为焦点.
以原点为顶点,椭圆的右焦点为焦点.
(Ⅰ)求椭圆 与抛物线
与抛物线 的方程;
的方程;
(Ⅱ)已知 ,
, 是椭圆
是椭圆 上两个不同点,且
上两个不同点,且 ⊥
⊥ ,判定原点
,判定原点 到直线
到直线 的距离是否为定值,若为定值求出定值,否则,说明理由.
的距离是否为定值,若为定值求出定值,否则,说明理由.
已知等差数列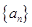 的首项
的首项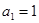 ,公差
,公差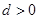 ,且
,且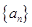 的第二项、第五项、第十四项成等比数列。
的第二项、第五项、第十四项成等比数列。
(1)求数列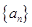 的通项公式;
的通项公式;
(2)设 ,记
,记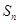 为数列
为数列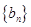 的前n项和,求
的前n项和,求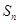 并说明是否存在最大的整数t,使得对任意的n均有
并说明是否存在最大的整数t,使得对任意的n均有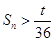 总成立?若存在,求出t;若不存在,请说明理由.
总成立?若存在,求出t;若不存在,请说明理由.
如图,在几何体 中,四边形
中,四边形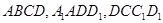 均为边长为1的正方形.
均为边长为1的正方形.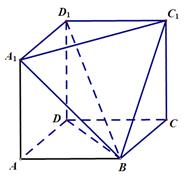
(1)求证: .
.
(2)求该几何体的体积.
已知函数
(1)求函数 的最小正周期和对称轴方程;
的最小正周期和对称轴方程;
(2)将 的图像左移
的图像左移 个单位,再向上移1个单位得到
个单位,再向上移1个单位得到 的图像,试求
的图像,试求 在区间
在区间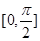 的值域.
的值域.
已知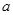 、
、 、c为正数,
、c为正数,
(1)若直线2x-(b-3)y+6=0与直线bx+ay-5=0互相垂直,试求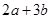 的最小值;
的最小值;
(2)求证: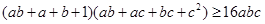 .
.