我市某工艺厂为迎“五一”,设计了一款成本为20元/件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价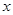 (元/件) (元/件) |
…… |
30 |
40 |
50 |
60 |
…… |
每天销售量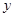 (件) (件) |
…… |
500 |
400 |
300 |
200 |
…… |
(1) 把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式; 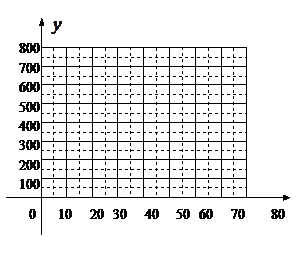
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.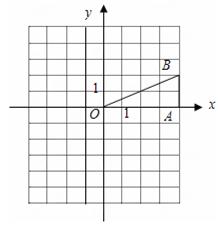
(1)画出将△OAB绕原点逆时针旋转90°后所得的△OA1B1,并写出点A1、B1的坐标;
(2)画出△OAB关于原点O的中心对称图形,并写出点A、B对称点的坐标.
已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,直线x=l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线x=l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线x=l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求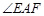 的度数.
的度数.
(2)如图②,在Rt△ABD中, ,
, ,点M,N是BD边上的任意两点,且
,点M,N是BD边上的任意两点,且 ,将△ABM绕点A逆时针旋转
,将△ABM绕点A逆时针旋转 至△ADH位置,连接
至△ADH位置,连接 ,试判断MN,ND,DH之间的数量关系,并说明理由.
,试判断MN,ND,DH之间的数量关系,并说明理由.
(3)在图①中,连接BD分别交AE,AF于点M,N,若 ,
, ,
, ,求AG,MN的长.
,求AG,MN的长.
某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
如图,AB是⊙O的直径,点F,C是⊙O上两点,且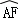 =
=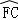 =
=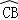 ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2 ,求⊙O的半径.
,求⊙O的半径.