如图,某小区准备绿化一块直径为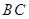 的半圆形空地,
的半圆形空地, 外的地方种草,
外的地方种草, 的内接正方形
的内接正方形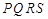 为一水池,其余地方种花.若
为一水池,其余地方种花.若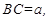
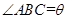 ,设
,设 的面积为
的面积为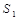 ,正方形
,正方形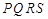 的面积为
的面积为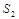 ,将比值
,将比值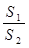 称为“规划合理度”.
称为“规划合理度”.
(1)试用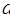 ,
,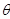 表示
表示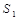 和
和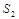 .
.
(2)当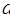 为定值,
为定值,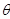 变化时,求“规划合理度”取得最小值时的角
变化时,求“规划合理度”取得最小值时的角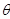 的大小.
的大小.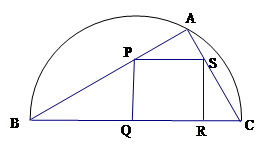
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.SD=2,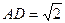 ,E是SD上的点。
,E是SD上的点。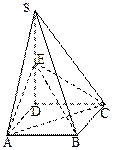
(Ⅰ)求证: AC⊥BE;
AC⊥BE;
(Ⅱ)求二面角C—AS—D的余弦值。
(本小题满分12分)已知函数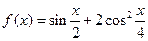
(1)求函数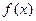 的最小正周期;
的最小正周期;
(2)在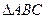 中,角
中,角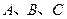 的分别是
的分别是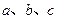 ,若
,若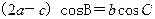 ,求
,求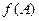 的取值范围
的取值范围
(本小题满分14分)已知函数f(x)=ln(x+a)-x2-x在x = 0处取得极值.
(Ⅰ)求实数a的值;
(Ⅱ)若关于x的方程,f(x)= 在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
(Ⅲ)证明:对任意的正整数n,不等式ln 都成立.
都成立.
(本小题满分12分)已知椭圆C: 过点
过点 ,且长轴长等于4.
,且长轴长等于4.
(Ⅰ)求椭圆C的方程;
(Ⅱ) 是椭圆C的两个焦点,⊙O是以F1F2为直径的圆,直线l: y=kx+m与⊙O相切,并与椭圆C交于不同的两点A、B,若
是椭圆C的两个焦点,⊙O是以F1F2为直径的圆,直线l: y=kx+m与⊙O相切,并与椭圆C交于不同的两点A、B,若 ,求
,求 的值
的值
定义在定义域D内的函数 ,若对任意的
,若对任意的
都有 则称函数
则称函数 为“Storm函数”。
为“Storm函数”。
已知函数
( 1 )若 求过点
求过点 处的切线方程;
处的切线方程;
( 2 )函数 是否为“Storm函数”?若是,给出证明;
是否为“Storm函数”?若是,给出证明;
若不是,说明理由。