已知,关于x的方程
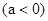 .
.求证:方程一定有两个不相等的实数根;
设方程的两个实数根分别为x1,x2(其中x1<x2),若y是关于a的函数,且
 ,求这个函数的解析式;
,求这个函数的解析式;在(2)的条件下,利用函数图像,求关于a的方程y+a+1=0的解
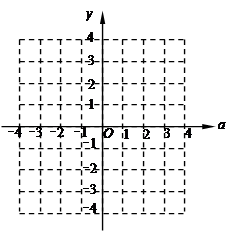
如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在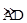 上.
上.
(1)求∠E的度数;
(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值.
已知关于x的方程x2-(k+1)x+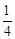 k2+1=0.
k2+1=0.
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两根恰好是一个矩形两邻边的长,且k=4,求该矩形的对角线的长.
小美和同学一起到游乐场游玩.游乐场的大型摩天轮的半径为20 m,匀速旋转1周需要12 min.小美乘坐最底部的车厢(离地面约0.5 m)开始1周的观光,请回答下列问题:(参考数据: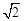 ≈1.414,
≈1.414,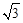 ≈1.732)
≈1.732)
(1)1.5min后小美离地面的高度是m;(精确到0.1m)
(2)摩天轮启动多长时间后,小美离地面的高度将首次达到10.5 m?
(3)摩天轮转动一周,小美在离地面10.5m以上的空中有多长时间?
某校为了解七年级学生课外学习情况,随机抽取了部分学生作调查,通过调查将获得的数据按性别绘制成如下的女生频数分布表和如图所示的男生频数分布直方图:
根据图表解答下列问题:
(1)在女生的频数分布表中,m=,n=;
(2)此次调查共抽取了多少名学生?
(3)从学习时间在120~150分钟的5名学生中依次抽取两名学生调查学习效率,恰好抽到男女生各一名的概率是多少?
如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20. 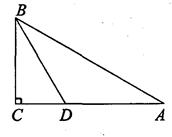
(1)求BC的长;
(2)求 的值.
的值.