如图,AB为⊙O的直径,点C在⊙O上,点D在AB的延长线上,且AC=CD,已知∠D=30°.
⑴判断CD与⊙O的位置关系,请说明理由
⑵若弦CF⊥AB,垂足为E,且CF= ,求图中阴影部分的面积.
,求图中阴影部分的面积.
实践应用(本小题满分6分)
有200名待业人员参加某企业甲、乙、丙三个部门的招聘,到各部门报名的人数百分比见图表1,该企业各部门的录取率见图表2.(部门录取率= ×100%)
×100%)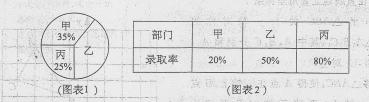
(1)到乙部门报名的人数有人,乙部门的录取人数是人,该企业的录取率为;
(2)如果到甲部门报名的人员中有一些人员改到丙部门报名,在保持各部门录取率不变的情况下,该企业的录取率将恰好增加15%,问有多少人从甲部门改到丙部门报名?
已知二次函数 的图象C1与x轴有且只有一个公共点.
的图象C1与x轴有且只有一个公共点.
(1)求C1的顶点坐标;
(2)将C1向下平移若干个单位后,得抛物线C2,如果C2与x轴的一个交点为A(—3,0),求C2的函数关系式,并求C2与x轴的另一个交点坐标;
(3)若 的取值范围.
的取值范围.
在直角坐标系xOy中,直线l过(1,3)和(3,1)两点,且与x轴,y轴分别交于A,B两点.
(1)求直线l的函数关系式;
(2)求△AOB的面积.
(本小题满分6分)
在如图所示的方格纸中,△ABC的顶点都在小正方形的顶点上,以小正方形互相垂直的两边所在直线建立直角坐标系.
(1)作出△ABC关于y轴对称的△A1B1C1,其中A,B,C分别和A1,B1,C1对应;
(2)平移△ABC,使得A点在x轴上,B点在y轴上,平移后的三角形记为△A2B2C2,作出平移后的△A2B2C2,其中A,B,C分别和A2,B2,C2对应;
(3)填空:在(2)中,设原△ABC的外心为M,△A2B2C2的外心为M,则M与M2之间的距离为.
推理证明(本小题满分6分)
如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D,AB=AD.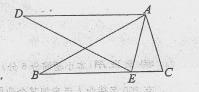
(1)求证:△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕着点A旋转一个锐角后与△ABC重合,求旋转角的大小.