如图,边长为2的正方形ABCD,E是BC的中点,沿AE,DE将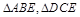 折起,使得B与C重合于O.
折起,使得B与C重合于O.
(Ⅰ)设Q为AE的中点,证明:QD AO;
AO;
(Ⅱ)求二面角O—AE—D的余弦值.
营养学家指出,成人良好的日常饮食应该至少提供7 5g碳水化合物,60g的蛋白质,60g的脂肪.1000g食物A含有105g碳水化合物,70g蛋白质,140g脂肪,花费28元;而1000g食物B含有105g碳水化
5g碳水化合物,60g的蛋白质,60g的脂肪.1000g食物A含有105g碳水化合物,70g蛋白质,140g脂肪,花费28元;而1000g食物B含有105g碳水化 合物,140g蛋白质,70g脂肪,花费21元.为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少g?花费多少钱?
合物,140g蛋白质,70g脂肪,花费21元.为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少g?花费多少钱?
已知函数 ,
,
(1)求不等式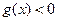 的解集;
的解集;
(2)若对一切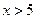 ,均有
,均有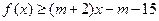 成立,求实数
成立,求实数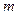 的取值范围.
的取值范围.
已知等差数列 的首项
的首项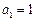 ,公差
,公差 .且
.且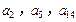 分别是等比数列
分别是等比数列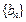 的
的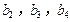
(1)求数列 与
与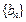 的通项公式;
的通项公式;
(2)设数列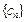 对任意自然数
对任意自然数
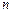 均有:
均有: 成立.求
成立.求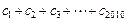 的值。
的值。
在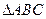 中,已知
中,已知 ,
,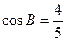 .
. (Ⅰ)求
(Ⅰ)求 的值
的值 ;
;
(Ⅱ)若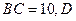 为
为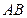 的中点,求
的中点,求 的长
的长
求数列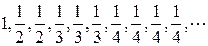
 的前100项
的前100项 的和。
的和。